Динамика машин и механизмов
|
Краткое содержание: Динамика машин и механизмов. Динамические параметры машины и механизма. Прямая и обратная задачи динамики. Механическая энергия и мощность. Работа внешних сил. Преобразование механической энергии механизмами. Аксиома об освобождения от связей. Силы и их классификация. Силы в КП без учета трения. Статический и кинетостатический силовой расчет типовых механизмов. Методы силового расчета (графоаналитический - планов сил, аналитический - метод проекций на оси координат).
Динамика машин и механизмов.
Динамика - раздел механики машин и механизмов, изучающий закономерности движения звеньев механизма под действием приложенных к ним сил. В [ ] дано такое определение: “Динамика рассматривает силы в качестве причины движения тел”.
В основе динамики лежат три закона, сформулированные Ньютоном, из которых следует:
Из первого закона: Если равнодействующая всех внешних сил, действующих на механическую систему равно нулю, то система находится в состоянии покоя.
Из второго закона: Изменение состояния движения механической системы может быть вызвано либо изменением действующих на нее внешних сил, либо изменением ее массы.
Из этих же законов следует, что динамическими параметрами механической системы являются:
инерциальные (массы m и моменты инерцииI);
силовые (силы Fij и моменты сил Mij);
кинематические (линейные a и угловые e ускорения).
В общей постановке динамика - изучение каких-либо процессов или явлений в функции времени. Динамическая модель - модель системы, предназначенная для исследования ее свойств в функции времени ( или модель системы, предназначенная для исследования в ней динамических явлений).
Прямая и обратная задачи динамики машин.
Прямая задача динамики - определение закона движения системы при заданном управляющем силовом воздействии.
Обратная задача динамики - определение требуемого управляющего силового воздействия, обеспечивающего заданный закон движения системы.
Методы составления уравнений (динамической модели системы):
энергетический (уравнения энергетического равновесия - закон сохранения энергия);
кинетостатический (уравнения силового равновесия с учетом сил инерции по принципу Д’Аламбера).
Механическая работа, энергия и мощность.
Работой называется интеграл скалярного произведения вектора силы F на вектор элементарного приращения перемещения точки ее приложения dS
где sk, s0-конечное и начальное перемещение точки приложения силы F,
( F,dS ) - острый угол между вектором силы F и вектором перемещения точки ее приложения dS.
Энергией называется способность системы совершать работу или запас работы. Любая работа совершаемая над системой увеличивает его энергию. В механических системах различают кинетическую и потенциальную энергии. Чтобы сообщить системе ускорение и заставить ее двигаться с требуемой скоростью, нужно совершить работу. Эта работа запасается системой в виде энергии движения или кинетической энергии. Для механической системы, в которой r звеньев вращаются, p совершают поступательное движение и k - плоское, кинетическая энергия равна:
где mi - масса i-го звена, Vsi - скорость центра масс i-го звена, Isi - момент инерции i-го звена относительно его центра масс, wi - угловая скорость i -го звена.
Перемещение системы или ее элемента в потенциальном поле из точки с низким потенциалом в точку с более высоким или деформация звена системы требует совершения работы, которая запасается системой в виде потенциальной энергии. Для системы, в которой a звеньев подвергаются скручиванию и s звеньев - линейной деформации, потенциальная энергия деформации равна:
где ci - крутильная жесткость i -го звена, dfi - угловая деформация i -го звена, ki - линейная жесткость i -го звена, dsi - линейная деформация i - го звена. Мощностью называется производная от работы по времени. Средняя мощность - отношение совершенной работы ко времени ее выполнения. Рассмотрим механическую систему на которую воздействуют m моментов и f сил. Элементарное приращение энергии системы (элементарная работа внешних сил, действующих на систему)
1. Механизм преобразующий вращательное движение во вращательное.
Освобождаясь от связей наложенных на исследуемую систему внешними системами, мы заменяем действие этих связей реакциями Fij , Fik и Fil. Силой называется мера механического воздействия одного материального тела на другое, характеризующая величину и направление этого воздействия. Т.е. сила - векторная величина, которая характеризуется величиной и направлением действия. Если одно тело действует с некоторой силой на другое тело, то на него со стороны последнего также действует сила, равная по величине и противоположно по направлению (третий закон Ньютона). Таким образом, силы всегда действуют парами, т.е. каждой силе Fij , действующей с тела i на тело j, соответствует противодействующая сила Fji. Согласно действующей договоренности, в индексе обозначения на первом месте указывается тело на которое действует сила, на втором - с которого. Классификация сил, действующих в механизмах. Все силы, действующие в механизмах, условно подразделяются на: внешние, действующие на исследуемую систему со стороны внешних систем и совершающие работу над системой. Эти силы в свою очередь подразделяются на: движущие, работа которых положительна (увеличивает энергию системы); сопротивления, работа которых отрицательна (уменьшает энергию системы). Силы сопротивления делятся на: силы полезного (технологического) сопротивления - возникающие при выполнении механической системы ее основных функций (выполнение требуемой работы по изменению координат, формы или свойств изделия и т.п.); силы трения (диссипативные) - возникающие в месте связи в КП и определяемые условиями физико-механического взаимодействия между звеньями (работа всегда отрицательна); взаимодействия с потенциальными полями (позиционные) - возникают при размещении объекта в потенциальном поле, величина зависит от потенциала точки, в которой размещается тело (работа при перемещении из точки с низким потенциалом в точку с более высоким - положительна; за цикл, т.е.
при возврате в исходное положение, работа равна нулю). Потенциальное поле - силы тяжести или веса. Существуют электромагнитные, электростатические и другие поля. внутренние, действующие между звеньями механической системы. Работа этих сил не изменяет энергии системы. В механических системах эти силы называются реакциями в КП. расчетные (теоретические) - силы, которые не существуют в реальности, а только используются в различных расчетах с целью их упрощения: силы инерции - предложены Д’Аламбером для силового расчета подвижных механических систем. При добавлении этих сил к внешним силам, действующим на систему, устанавливается квазистатическое равновесие системы и ее можно рассчитывать, используя уравнения статики (метод кинетостатики). приведенные (обобщенные) силы - силы. совершающие работу по обобщенной координате равную работе соответствующей реальной силы на эквивалентном перемещении точки ее приложения. Необходимо отметить, что под силами понимаются равнодействующие соответствующих распределенных в месте контакта КП нагрузок. Все вышесказанное относительно сил распространяется и на моменты сил. Силы в кинематических парах плоских механизмов (без учета трения). Сила, как векторная величина характеризуется относительно звеньев механизма тремя параметрами: координатами точки приложения, величиной и направлением. Рассмотрим с этих позиций реакции в КП плоских механизмов. 1. Поступательная КП. В поступательной КП связи, наложенные на относительное движение звеньев запрещают относительное поступательное движение по оси y и относительное вращение. Заменяя эти связи реакциями, получим реакцию Fij и реактивный момент Mij (см. рис. 4.4).
При силовом расчете поступательной КП определяются: реактивный момент Mij, величина реакции Fij
известны: точка приложения силы - геометрический центр кинематической пары A1 п.и направление - нормаль к контактирующим поверхностям звеньев.
Число связей в КП Sпл = 2, подвижность звеньев в КП Wпл =1, число неизвестных при силовом расчете ns = 2. 2.
Вращательная КП. Во вращательной КП связи, наложенные на относительное движение звеньев запрещают относительное поступательное движение по осям y и x. Заменяя эти связи реакциями, получим реакцию Fij (см. рис. 4.5).
При силовом расчете поступательной КП определяются: направление реакцииFij;
величина реакции Fij;
известна: точка приложения силы - геометрический центр кинематической пары B1 в..
Число связей в КП Sпл = 2, подвижность звеньев в КП Wпл=1, число неизвестных при силовом расчете ns = 2. 3. Высшая КП. В высшей паре связи,наложенные на относительное движение звеньев, запрещают движение в направлении нормали к контактирующим поверхностям (ось y). Заменяя эту связь реакцией, получим реакцию Fij (см.рис. 4.5).
При силовом расчете в высшей КП определяются: величина реакции Fij; известны: точка приложения силы - точка контакта рабочих профилей кинематической пары С2вп;
направление вектора силы - контактная нормаль к профилям.
Число связей в КП S пл = 1, подвижность звеньев в КП Wпл =2, число неизвестных при силовом расчете ns = 1. Силовой расчет типовых механизмов. Постановка задачи силового расчета: для исследуемого механизма при известных кинематических характеристиках и внешних силах определить уравновешивающую силу или момент (управляющее силовое воздействие) и реакции в кинематических парах механизма. Виды силового расчета: статический - для механизмов находящихся в покое или движущихся с малыми скоростями, когда инерционные силы пренебрежимо малы, или в случаях, когда неизвестны массы и моменты инерции звеньев механизма (на этапах, предшествующих эскизному проектированию); Уравнения статического равновесия:
где Fi - внешние силы, приложенные к механизму или его звеьям,
Mi- внешние моменты сил, приложенные к механизму или его звеьям. кинетостатический - для движущихся механизмов при известных массах и моментах инерции звеньев, когда пренебрежение инерционными силами приводит к существенным погрешностям; Уравнения кинетостатического равновесия:
где Fиi-инерционные силы, приложенные к звеньям, Mиi-моменты сил инерции, приложенные к звеньям. кинетостатический с учетом трения - может быть проведен когда определены характеристики трения в КП и размеры элементов пар. Определение числа неизвестных при силовом расчете. Для определения числа неизвестных, а, следовательно, и числа независимых уравнений, при силовых расчетах необходимо провести структурный анализ механизма и определить число и классы кинематических пар, число основных подвижностей механизма, число избыточных связей. Чтобы силовой расчет можно было провести, используя только уравнения кинетостатики, необходимо устранить в нем избыточные связи. В противном случае, к системе уравнений кинетостатики необходимо добавить уравнения деформации звеньев, необходимые для раскрытия статической неопределимости механизма. Так как каждая связь в КП механизма соответствует одной компоненте реакции, то число неизвестных компонент реакций равно суммарному числу связей накладываемых КП механизма. Уравновешивающая сила или момент должны действовать по каждой основной подвижности механизма. Поэтому суммарное число неизвестных в силовом расчете определяется суммой связей в КП механизма и его основных подвижностей
где ns- число неизвестных в силовом расчете. Кинетостатический силовой расчет типовых механизмов. Рассмотрим механизм, состоящий из трех соединенных последовательно простых механизмов: зубчатой передачи, кулачкового механизма и четырехшарнирного рычажного механизма (рис. 4.6).
Представим этот механизм в виде комбинации типовых механизмов:
1.Кинетостатический расчет зубчатой передачи (метод планов сил).
Для примера рассмотрим цилиндрическую эвольвентную зубчатую передачу. При проведении расчета нам необходима информация о размерах зубчатых колес и положении контактной нормали в высшей КП. Для эвольвентной передачи необходимо знать радиусы основных rb1 ,rb2или начальных окружностей rw1 ,rw2, и угол зацепления aw, т.к rbi =rw1 ?cos aw . По этим размерам в масштабе изображается кинематическая схема механизма, на которую наносятся все известные силы и моменты.
Главные вектора и моменты сил инерции рассчитываются по формулам
Определим подвижность, число избыточных связей в механизме, а также число неизвестных в силовом расчете:
т.е в нашем механизме неизвестно 6 компонент реакций, для решения задачи силового расчета необходимо составить 6 уравнений кинетостатики. Структурный анализ механизма показывает что механизм состоит из одного первичного механизма (звено 1 и стойка) и монады (структурной группы, состоящей из одного звена 2). Анализ начнем со второго звена, так как о нем больше известно.
Расчетная схема для звена 2 приведена на рис. 4.9.
>Уравнения равновесия для звена 2: векторное уравнение силового равновесия
Расчетная схема для звена 1 приведена на рис. 4.11.
Уравнения равновесия для звена 1: векторное уравнение силового равновесия
Дано: >li, j3, w3, e3, mi, Isi, Mc5.
Определить:Fij, Mд3. 1. Определение подвижности механизма, числа избыточных связей в КП и числа неизвестных в силовом расчете.
Кинетостатический расчет механизма. 4.1 Звено 5 (рис. 4.14).
Уравнения силового равновесия в проекциях на оси координат
и сумма моментов сил относительно точки L
Уравнения силового равновесия в проекциях на оси координат
и сумма моментов сил относительно точки Q
и сумма моментов сил относительно точки C
Эвольвентное зубчатое колесо и его параметры
|
Краткое содержание: Эвольвентное зубчатое колесо и его параметры. Толщина зуба колеса по окружности произвольного радиуса. Методы изготовления эвольвентных зубчатых колес. Понятие о исходном, исходном производящем и производящем контурах. Станочное зацепление. Основные размеры зубчатого колеса. Виды зубчатых колес. Подрезание и заострение колеса. Понятие о области существования зубчатого колеса. Эвольвентная цилиндрическая зубчатая передача и ее параметры. Основные уравнения эвольвентного зацепления.
Эвольвентное зубчатое колесо и его параметры.
Эвольвентным зубчатым колесом называют звено зубчатого механизма, снабженное замкнутой системой зубьев. При проектировании зубчатого колеса вначале нужно определить его число зубьев z, а затем определить параметры зубьев. Для этого нужно произвольную окружность колеса ry разделить на z частей, каждая из которых называется окружным шагом py.
2*p * ry = py* z => 2* ry = (py/p )* z = my* z = dy ,
где my= py /p = dy / z - модуль зацепления по окружности произвольного радиуса.
Модулем зацепления называется линейная величина в p раз меньшая окружного шага или отношение шага по любой концентрической окружности зубчатого колеса к p . В зависимости от окружности по которой определен модуль различают делительный, основной, начальный. Для косозубых колес еще и нормальный, торцевой и осевой модули. В ряде стран используется величина обратная модулю, которая называется питчем. Питч (диаметральный) - число зубьев колеса, приходящееся на дюйм диаметра. Исходя из этого модуль можно определить как число милиметров диаметра, приходящееся на один зуб. На колесе можно провести бесчисленное число окружностей на каждой из которых будет свой модуль. Для ограничения этого числа ГОСТом введен стандартный ряд модулей. Стандартной модуль определяется по окружности называемой делительной. Точнее делительной называется такая окружность зубчатого колеса, на которой модуль и шаг принимают стандартное значение. Окружным шагом или шагом называется расстояние по дуге окружности между одноименными точками профилей соседних зубьев (под одноименными понимаются правые или левые профили зуба).
Угловой шаг t - центральный угол соответствующий дуге p - окружному шагу по делительной окружности.
Примечание: Согласно ГОСТ основные элементы зубчатого колеса обозначаются по следующим правилам: линейные величины - строчными буквами латинского алфавита, угловые - греческими буками; установлены индексы для величин :
по окружностям: делительной - без индекса, вершин - a , впадин - f , основная - b , начальная - w , нижних точек активных профилей колес - p , граничных точек - l ;
по сечениям: нормальное сечение - n , торцевое сечение - t , осевое сечение - x ;
относящихся к зуборезному инструменту - 0 .
Для параметров зубчатого колеса справедливы следующие соотношения
dy = my* z - диаметр окружности произвольного радиуса,
d = m* z - диаметр делительной окружности,
py = my* p - шаг по окружности произвольного радиуса,
p = m* p - шаг по делительной окружности,
a y - угол профиля на окружности произвольного радиуса.
Углом профиля называется острый угол между касательной к профилю в данной точки и радиусом - вектором, проведенным в данную точку из центра колеса.
Шаг колеса делится на толщину зуба sy и ширину впадины ey . Толщина зуба sy - расстояние по дуге окружности ry между разноименными точками профилей зуба. Ширина впадины ey - расстояние по дуге окружности ry между разноименными точками профилей соседних зубьев.
На основной окружности a b=> 0 и cos a b=> 1, тогда
mb = m* cos a =>pb = p * m* cos a .
В зависимости от соотношения между толщиной зуба и шириной впадины на делительной окружности зубчатые колеса делятся на:
нулевые s = e = p * m / 2 , D = 0;
положительные s > e , =>D > 0;
отрицательные s < e , => D < 0;
где D - коэффициент изменения толщины зуба (отношение приращения толщины зуба к модулю). Тогда толщину зуба по делительной окружности можно записать
s = (p * m / 2 ) + D * m = m*[(p / 2 ) + D ].
Более подробно познакомиться с основными определениями и расчетными зависимостями можно в литературе [ 11.1 ] и в ГОСТ 16530-83.
Толщина зуба колеса по окружности произвольного радиуса.
s = (p * m / 2 ) + D * m.
Угловая толщина зуба по окружности произвольного радиуса из схемы на рис. 11.2
sy / ry = s / r - ( inv a y - inv a )* 2,
где r = m*z / 2 , ry = m*z * cos a / (2* cos a y )
Подставляя в формулу угловой толщины эти зависимости, получим
sy = s* ry / r - ( inv a y - inv a )* 2* ry,
или
sy = m * (cos a / cos a y) * [(p / 2 ) + D - ( inv a y - inv a )* z] .
Методы изготовления эвольвентных зубчатых колес.
Существует множество вариантов изготовления зубчатых колес. В их основу положены два принципиально отличных метода:
метод копирования, при котором рабочие кромки инструмента по форме соответствуют обрабатываемой поверхности ( конгруентны ей, т. е. заполняют эту поверхность как отливка заполняет форму ); метод огибания, при котором инструмент и заготовка за счет кинематической цепи станка выполняют два движения - резания и огибания (под огибанием понимается такое относительное движение заготовки и инструмента , которое соответствует станочному зацеплению, т. е. зацеплению инструмента и заготовки с требуемым законом изменения передаточного отношения). Из вариантов изготовления по способу копирования можно отметить:
Нарезание зубчатого колеса профилированной дисковой или пальцевой фрезой (проекция режущих кромок которой соответствует конфигурации впадин). При этом методе резание производится в следующем прядке: прорезается впадина первого зуба, затем заготовка с помощью делительного устройства (делительной головки) поворачивается на угловой шаг и прорезается следующая впадина. Операции повторяются пока не будут прорезаны все впадины. Производительность данного способа низкая, точность и качество поверхности невысокие. Отливка зубчатого колеса в форму. При этом внутренняя поверхность литейной формы конгруентна наружной поверхности зубчатого колеса. Производительность и точность метода высокая, однако при этом нельзя получить высокой прочности и твердости зубьев.
Из вариантов изготовления по способу огибания наибольшее распространение имеют:
Обработка на зубофрезерных или зубодолбежных станках червячными фрезами или долбяками. Производительность достаточно высокая, точность изготовления и чистота поверхностей средняя. Можно обрабатывать колеса из материалов с невысокой твердостью поверхности. Накатка зубьев с помощью специального профилированного инструмента. Обеспечивает высокую производительность и хорошую чистоту поверхности. Применяется для пластичных материалов, обычно на этапах черновой обработки. Недостаток метода образование наклепанного поверхностного слоя, который после окончания обработки изменяет свои размеры. Обработка на зубошлифовальных станках дисковыми кругами. Применяемся как окончательная операция после зубонарезания (или накатки зубьев) и термической обработки. Обеспечивает высокую точность и чистоту поверхности. Применяется для материалов с высокой поверхностной прочностью. Понятие о исходном, исходном производящем и производящем контурах .
Для сокращения номенклатуры режущего инструмента стандарт устанавливает нормативный ряд модулей и определенные соотношения между размерами элементов зуба. Эти соотношения определяются:
для зубчатых колес определяются параметрами исходной рейки через параметры ее нормального сечения - исходный контур; для зубчатого инструмента определяются параметрами исходной производящей рейки через параметры ее нормального сечения - исходный производящий контур.
угол главного профиля a = 20° ; коэффициент высоты зуба h*a = 1 ; коэффициент высоты ножки h*f = 1.25 ; коэффициент граничной высоты h*l = 2 ; коэффициент радиуса кривизны переходной кривой r *f =с */(1-sina )= 0.38 ; коэффициент радиального зазора в паре исходных контуров с * = 0.25. Исходный производящий контур отличается от исходного высотой зуба h0 = 2.5m.
Исходный и исходный производящий контуры образуют между собой конруентную пару (рис. 12.3), т.е.
один заполняет другой как отливка заполняет заготовку (с радиальным зазором с **m в зоне прямой вершин зуба исходной рейки). Принципиальное отличие этих контуров в том, что исходный контур положен в основу стандартизации зубчатых колес, а исходный производящий - в основу стандартизации зуборезного инструмента. Оба эти контура необходимо отличать от производящего контура - проекции режущих кромок инструмента на плоскость перпендикулярную оси заготовки.
Станочное зацепление.
Станочным зацеплением называется зацепление, образованное заготовкой колеса и инструментом, при изготовлении зубчатого колеса на зубообрабатывающем оборудовании по способу обката. Схема станочного зацепления колеса и инструмента с производящим контуром, совпадающим с исходным производящим контуром, изображена на рис. 12.4.
Смещение исходного производящего контура x*m - кратчайшее расстояние между делительной окружностью заготовки и делительной прямой исходного производящего контура.
Уравнительное смещение D y*m - условная расчетная величина, введенная в расчет геометрии зацепления с целью обеспечения стандартного радиального зазора в зацеплении (величина, выражающая в долях модуля уменьшение радиуса окружностей вершин колес, необходимое для обеспечения стандартной величины радиального зазора).
Окружность граничных точек rl - окружность проходящая через точки сопряжения эвольвентной части профиля зуба с переходной кривой.
Основные размеры зубчатого колеса.
Определим основные размеры эвольвентного зубчатого колеса, используя схему станочного зацепления (рис. 12.4).
Радиус окружности вершин ra = r + h*a* m + x* m - D y* m ; r = m * z / 2 ;
ra = m * ( z / 2 + h*a + x - D y ) .
Высота зуба h = c** m + 2* h*a* m - D y* m ;
h = m * ( c* + 2* h*a - D y ) .
Радиус окружности впадин rf = r a - h = m * (z/2 - h*a - c* + x ) .
Толщина зуба по делительной окружности. Так как стночно-начальная прямая перекатывается в процессе огибания по делительной окружности без скольжения, то дуга s-s по делительной окружности колеса равна ширине впадины e-e по станочно-начальной прямой инструмента. Тогда, c учетом схемы на рис. 12.5, можно записать
s = e0 + 2* x * m * tg a ,
s = m * ( p / 2 + 2* x * tg a ),
где D = 2* x * tg a .
Виды зубчатых колес (Классификация по величине смещения).
В зависимости от расположения исходного производящего контура относительно заготовки зубчатого колеса, зубчатые колеса делятся на нулевые или без смещения, положительные или с положительным смещением, отрицательные или с отрицательным смещением.
Подрезание и заострение зубчатого колеса.
Если при нарезании зубчатого колеса увеличивать смещение, то основная и делительная окружность не изменяют своего размера, а окружности вершин и впадин увеличиваются. При этом участок эвольвенты, который используется для профиля зуба, увеличивает свой радиус кривизны и профильный угол. Толщина зуба по делительной окружности увеличивается , а по окружности вершин уменьшается.
x2 > x1 => ra2 > ra1 ;
s2 > s1 => sa2 < sa1 .
Для термобработанных зубчатых колес с высокой поверхностной прочностью зуба заострение вершины зуба является нежелательным. Термообработка зубьев (азотирова-ние, цементация, цианирование), обеспечивающая высо Рис. 12.7 кую поверхностную прочность и твердость зубьев при сохранении вязкой серцевины, осуществляется за счет насыщения поверхностных слоев углеродом. Вершины зубьев, как выступающие элементы колеса, насыщаются углеродом больше. Поэтому после закалки они становятся более твердыми и хрупкими. У заостренных зубьев появляется склонность к скалыванию зубьев на вершинах. Поэтому рекомендуется при изготовлении не допускать толщин зубьев меньших некоторых допустимых значений. То есть заостренным считается зуб у которого
sa < [sa], где sa = m*(cos a / cos a a )*[(p /2 )+ D - ( inv a a - inv a )* z] .
При этом удобнее пользоваться относительными величинами [sa /m ]. Обычно принимают следующие допустимые значения
улучшение, нормализация [sa /m ] = 0.2;
цианирование, азотирование [sa /m ] = 0.25...0.3;
цементация [sa /m ] = 0.35...0.4.
Подрезание эвольвентных зубьев в станочном зацеплении.
В процессе формирования эвольвентного зуба по способу огибания, в зависимости от взаимного расположения инструмента и заготовки возможно срезание эвольвентной части профиля зуба той частью профиля инструмента, которая формирует переходную кривую. Условие при котором это возможно определяется из схемы станочного зацепления. Участок линии зацепления, соответствующий эвольвентному зацеплению определяется отрезком B1. где точка Bl определяется пересечением линии станочного зацепления и прямой граничных точек инструмента. Если точка Bl располагается ниже (см. рис.12.8) точки N , то возникает подрезание зуба. Условие при котором нет подрезания можно записать так
P0N > P0Bl .
Из D P0N0
P0N = r * sin a = m*z*sin a / 2,
а из D P0BlF
P0Bl = ( h*a - x )* m / sin a .
Тогда
z*sin a / 2 > ( h*a - x ) / sin a ,
при x=0
z > 2 * h*a / sin2 a ,
zmin = 2 * h*a / sin2 a ,
где zmin - минимальное число зубьев нулевого колеса нарезаемое без подрезания.
Избежать подрезания колеса можно если увеличить смещение инструмент так, чтобы точка Bl оказалась бы выше точки N или совпала с ней. Тогда смещение инструмента при котором не будет подрезания
x > h*a - z * sin2 a / 2 , => x > h*a * [ 1 - z * sin2 a / (2* h*a )],
x > h*a * ( 1 - z / z min ).
В предельном случае, когда точка Bl совпадает с точкой N
xmin = h*a * ( 1 - z / z min ),
где xmin - минимальное смещение инструмента при котором нет подрезания.
Параметры в зубчатых передачах удобно разделять на параметры зубчатого колеса и параметры зубчатой передачи.
Параметры зубчатого колеса характеризуют данное зубчатое колесо и, как составная часть, входят в параметры зубчатой передачи, образованной этим колесом с другим парным ему колесом. К параметрам зубчатого колеса относятся: число зубьев, модуль, параметры исходного контура инструмента, которым оно обрабатывалось и коэффициент смещения. Как отмечено выше, на выбор этих параметров накладываются ограничения по заострению и подрезанию зуба. Поэтому можно ввести понятие области существования зубчатого колеса - диапазона коэффициентов смещения при которых не будет подрезания и заострения. На рис. 12.11 показан пример такой области существования.
Два зубчатых колеса с одинаковым модулем и с числами зубьев соответствующими заданному передаточному отношению образуют зубчатую передачу или простейший зубчатый механизм. В этом трехзвенном механизме зубчатые колеса образуют между собой высшую пару, а со стойкой низшие пары. Зубчатая передача, кроме параметров образующих ее колес, имеет и собственные параметры: угол зацепления a w, межосевое расстояние aw, воспринимаемое смещение y*m и уравнительное смещение D y*m . Передаточное отношение механизма u12, числа зубьев колес z1 и z2, начальные окружности rw1 и rw2(или центроиды) и межосевое расстояние aw связаны между собой следующими соотношениями ( см. основную теорему зацепления и раздел по кинематике зубчатой передачи):
aw = rw1 + rw2 ; u12 = rw2 / rw1 ; aw = rw1 * ( 1 + u12 ) ;
rw1= aw /( 1 + u12); rw2 = rw1 - aw .
Изобразим схему зацепления эвольвентной зубчатой передачи (рис.12.12).
1. Угол зацепления a w
Так как перекатывание начальных окружностей друг по другу происходит без скольжения, то
sw1 = ew2 и sw2 = ew1 , но sw1 + ew1 = pw1 и sw2 + ew2 = pw2 ,
кроме того pw1= pw2= pw , тогда sw2 + sw1 = pw .
Толщину зуба по начальной окружности можно записать, используя формулу для толщины зуба по окружности произвольного радиуса
sw1 = m * (cos a / cos a w) * [(p / 2 ) + D 1 - ( inv a w - inv a )* z1 ] ,
sw2 = m * (cos a / cos a w) * [(p / 2 ) + D 2 - ( inv a w - inv a )* z2 ] ,
а шаг по начальной окружности равен
pw = p * m * (cos a / cos a w).
Поставляя эти выражения в формулу для шага по начальной окружности, получим
pw = sw2 + sw1 p * m * (cos a / cos a w ) = m * (cos a / cos a w) *[(p / 2 ) + D 2 - ( inv a w - inv a )* z2 + (p / 2 ) + D 1 - ( inv a w - inv a )* z1 ]
(D 1 + D 2) - (z1 + z2) * ( inv a w - inv a ) = 0,
inv a w = inv a + ( D 1 + D 2 )/ ( z1 + z2 ).
2. Межосевое расстояние aw
Из схемы эвольвентного зацепления (рис.12.12) можно записать
aw = rw1 + rw2 ,
но ry = r * (cos a / cos a y ) и rw = r * (cos a / cos a w ),
после подстановки, получим
aw = r1 * (cos a / cos a w ) + r2 * (cos a / cos a w ) ,
aw = ( m*z1 /2 + m*z2 / 2 )* (cos a / cos a w ) ,
aw = m* (z1 + z2 )* (cos a / cos a w ) / 2 .
3. Воспринимаемое смещение y* m
Из схемы эвольвентного зацепления (рис.12.12) можно записать
Из рис. 12.12 aw = ra1 + c** m + rf2 ,
aw = r1 + r2 + y* m ,
откуда
ra1 + c** m + rf2 = r1 + r2 + y* m ,
где ra1 = m * ( z1 / 2 + h*a + x1 - D y ), rf 2= m * (z2 /2 - h*a - c* + x2 ) .
Подставим эти выражения
x1 + x2 - D y = y,
D y = ( x1 + x2 ) - y.
Литература.
В.А.Гавриленко . Зубчатые передачи в машиностроении (Теория эвольвентных зубчатых передач). М.: Машгиз - 1962, 530 стр., илл. Ф.Л.Литвин Теория зубчатых зацеплений. Изд. 2-е, перераб. и доп. М.: - Наука - 1968, 584 стр., илл.
Классификация кинематических пар
|
Краткое содержание: Классификация кинематических пар. Модели машин. Методы исследования механизмов. Понятие о структурном анализе и синтезе. Основные структурные формулы. Структурная классификация механизмов по Ассуру и по Артоболевскому. Структурный анализ механизма. Подвижности и связи в механизме. Понятие об избыточных связях и местных подвижностях. Рациональная структура механизма. Методы определения и устранения избыточных связей и местных подвижностей.
Классификация кинематических пар.
Кинематические пары (КП) классифицируются по следующим признакам:
по виду места контакта (места связи) поверхностей звеньев: низшие, в которых контакт звеньев осуществляется по плоскости или поверхности ( пары скольжения ); высшие, в которых контакт звеньев осуществляется по линиям или точкам (пары, допускающие скольжение с перекатыванием).по относительному движению звеньев, образующих пару: вращательные; поступательные; винтовые; плоские; сферические.
по способу замыкания (обеспечения контакта звеньев пары): силовое (за счет действия сил веса или силы упругости пружины); геометрическое (за счет конструкции рабочих поверхностей пары).
 |
 |
| Рис. 2.1 | Рис. 2.2 |
по числу условий связи, накладываемых на относительное движение звеньев ( число условий связи определяет класс кинематической пары );
по числу подвижностей в относительном движении звеньев.
Классификация КП по числу подвижностей и по числу связей приведена в таблице 2.1.
Классификация кинематических пар по числу связей и по подвижности.
Таблица 2.1
| Класс пары | Число связей | Подвижность | Пространственная схема (пример) | Условные обозначения |
| I | 1 | 5 |  |
 |
| II | 2 | 4 |  |
 |
| III | 3 | 3 |  |
 |
| IV | 4 | 2 |  |
 |
| V | 5 | 2 |  |
 |
Примечание: Стрелки у координатных осей показывают возможные угловые и линейные относительные перемещения звеньев. Если стрелка перечеркнута, то данное движение в КП запрещено (т.е. на данное относительное движение наложена связь).
Модели машин.
Модель (от лат. modulus - мера, образец) - устройство или образ ( мысленный или условный: схема, чертеж, система уравнений и т.п.) какого-либо объекта или явления (оригинала данной модели), адекватно отражающей его исследуемые свойства и используемый в качестве заместителя объекта в научных или иных целях (рис.2.3).
 |
| Рис. 2.3 |
Виды моделей.
По форме представления: физические; математические: аналоговые; цифровые.
По назначению: функциональные; структурные; геометрические; кинематические; динамические.
По методу исследования: графические; численные; графо-аналитические; энергетические; кинето-статические; экспериментальные. Структура механизмов.
Как отмечалось выше, структура любой технической системы определяется функционально связанной совокупностью элементов и отношений между ними. При этом для механизмов под элементами понимаются звенья, группы звеньев или типовые механизмы, а под отношениями подвижные (КП) или неподвижные соединения. Поэтому под структурой механизма понимается совокупность его элементов и отношений между ними, т.е. совокупность звеньев, групп или типовых механизмов и подвижных или неподвижных соединений. Геометрическая структура механизма полностью описывается заданием геометрической формы его элементов, их расположения, указания вида связей между ними. Структура механизма может быть на разных стадиях проектирования описываться различными средствами, с разным уровнем абстрагирования: на функциональном уровне - функциональная схема, на уровне звеньев и структурных групп - структурная схема и т.п. Структурная схема - графическое изображение механизма, выполненное с использованием условных обозначений рекомендованных ГОСТ (см. например ГОСТ 2.703-68) или принятых в специальной литературе, содержащее информацию о числе и расположении элементов (звеньев, групп), а также о виде и классе кинематических пар, соединяющих эти элементы. В отличие от кинематической схемы механизма, структурная схема не содержит информации о размерах звеньев и вычерчивается без соблюдения масштабов. (Примечание: кинематическая схема - графическая модель механизма, предназначенная для исследования его кинематики.)
Понятие о структурном синтезе и анализе.
Как на любом этапе проектирования при структурном синтезе различают задачи синтеза и задачи анализа.
Задачей структурного анализа является задача определения параметров структуры заданного механизма - числа звеньев и структурных групп, числа и вида КП, числа подвижностей (основных и местных), числа контуров и числа избыточных связей.
Задачей структурного синтеза является задача синтеза структуры нового механизма, обладающего заданными свойствами: числом подвижностей, отсутствием местных подвижностей и избыточных связей, минимумом числа звеньев, с парами определенного вида (например, только вращательными, как наиболее технологичными) и т.п.
Основные понятия структурного синтеза и анализа.
Подвижность механизма - число независимых обобщенных координат однозначно определяющее положение звеньев механизма на плоскости или в пространстве.
Связь - ограничение, наложенное на перемещение тела по данной координате.
Избыточные (пассивные) - такие связи в механизме, которые повторяют или дублируют связи, уже имеющиеся по данной координате, и поэтому не изменяющие реальной подвижности механизма. При этом расчетная подвижность механизма уменьшается, а степень его статической неопределимости увеличивается. Иногда используется иное определение: Избыточные связи - это связи число которых в механизме определяется разностью между суммарным числом связей, наложенных кинематическими парами, и суммой степеней подвижности всех звеньев, местных подвижностей и заданной (требуемой) подвижностью механизма в целом.
Местные подвижности - подвижности механизма, которые не оказывают влияния на его функцию положения (и передаточные функции), а введены в механизм с другими целями (например, подвижность ролика в кулачковом механизме обеспечивает замену в высшей паре трения скольжения трением качения).
Основные структурные формулы.
Основные структурные формулы были составлены для плоских механизмов Чебышевым П.Л.
и Грюблером М., для пространственных - Сомовым П.О. и Малышевым. Так как принципы заложенные в построение всех этих формул одинаковы, то их можно записать в обобщенном виде:
H-1
W = H*n + S (H-i) * pi ,
i=1
| где: | H - число степеней подвижности твердого тела (соответственно при рассмотрении механизма в пространстве H=6, на плоскости H=3); n - число подвижных звеньев в механизме; n = k - 1; k - общее число звеньев механизма (включая и неподвижное звено - стойку); i - число подвижностей в КП; pi - число кинематических пар с i подвижностями. |
q = W0+ Wм - W,
| где: | q - число избыточных связей в механизме; W0 - заданная или требуемая подвижность механизма; Wм - число местных подвижностей в механизме; W - расчетная подвижность механизма. |
Пример структурного анализа механизма.
 |
| Рис. 2.4 |
Функциональная схема на уровне типовых механизмов.
 |
| Рис. 2.5 |
На рис.2.4 изображена структурная схема плоского механизма долбежного станка, а на рис.2.5 его функциональная схема на уровне типовых механизмов. Структурная схема механизма в соответствии с принятыми условными обозначениями изображает звенья механизма, их взаимное расположение, а также подвижные и неподвижные соединения между звеньями. На схеме звенья обозначены цифрами, кинематические пары - заглавными латинскими буквами. Цифры в индексах обозначения КП указывают относительную подвижность звеньев в паре, буквы - на вид пары, который определяется видом относительного движения звеньев (в - вращательное, п - поступательное, ц - цилиндрическое, вп - обозначает высшую пару в которой возможно относительное скольжение с одновременным перекатыванием). Схема на рис. 2.5 отражает структуру механизма в виде последовательного и параллельного соединения простых или типовых механизмов. В этом механизме вращательное движение вала двигателя f1 в согласованные движения подачи f8 и долбяка S6.
При этом механическая энергия двигателя преобразуется: скоростные составляющие энергетического потока по величине уменьшаются, а силовые - увеличиваются. Структурные элементы (типовые механизмы) в этой схеме связаны между собой неподвижными соединениями - муфтами. Схема показывает из каких простых механизмов состоит исследуемый, как эти механизмы взаимосвязаны между собой (последовательно или параллельно), как происходит преобразование входных движений в выходные (в нашем примере f1 в f8 и S6).
Проведем структурный анализ данного механизма. Число подвижных звеньев механизма n=8, числокинематических пар pi=12, из них для плоского механизма одноподвижных p1=10 (вращательных p1в=8, поступательных p1п=2 и двухподвижных p2=2. Число подвижностей механизма на плоскости:
Wпл = 3*8 - (2*10 + 1*2) = 2 = 1 + 1,
полученные две подвижности делятся на основную или заданную W0 = 1 и местную Wм = 1. Основная подвижность определяет основную функцию механизма преобразование входного движения f1 в два функционально взаимосвязанных f8 и S6. Местная обеспечивает выполнение вспомогательной функции: заменяет в высшей паре кулачок - толкатель трение скольжения трением качения. Если рассматривать механизм как пространственный, то во-первых необходимо учесть, что с увеличением подвижности звеньев с трех до шести изменяются и подвижности некоторых кинематических пар. В нашем примере это высшие пары K и P, подвижность которых изменяется с двух до четырех, и низшая пара D, у которой подвижность увеличивается до двух. С учетом сказанного, подвижность пространственного механизма равна:
Wпр = 6*8 - (4*1 + 5*9 + 2*2) = 48 - 53 = -5,
т. е. как пространственный данный механизм не имеет подвижности, так как число связей в нем существенно (на пять) превышает суммарную подвижность всех его звеньев. Однако от рассмотренного ранее плоского варианта пространственный механизм ничем не отличается, то есть он имеет две подвижности основную и местную. Как отмечено, выше связи, не изменяющие подвижности механизма, являются пассивными или избыточными.
Для нашего механизма чилсло избыточных связей:
на плоскости
qпл = W0 + Wм - Wпл = 1 + 1 - 2 = 0;
в пространстве
qпр = W0 + Wм - Wпр = 1 + 1 - (-5) = 7.
Возникает вопрос: почему при переходе от плоской к пространственной модели механизма возникают избыточные связи? При анализе плоской модели механизма мы исключаем из рассмотрения три координаты, а , следовательно, и связи наложенные по этим координатам. В плоском механизме априорно задано, что оси всех вращательных и высших пар перпендикулярны, а оси поступательных параллельны плоскости, в которой рассматривается механизм. При пространственном анализе механизма это условие отсутствует. В нашем механизме 12 кинематических пар и , следовательно, 12 таких условий. Если учесть, что при переходе от плоской модели к пространственной общее число подвижностей в КП увеличилось на пять, то получим семь избыточных связей (т.к. 12 - 5 = 7). Известно, что избыточные связи возникают только в замкнутых кинематических цепях. Поэтому при анализе структуры механизма важно знать число независимых контуров, образованных его звеньями. Независимым считается контур отличающийся от остальных хотя бы на одно звено. Расчет числа контуров для механизма проводят по формуле Гохмана Х.И.:
K = pi - n = 12 - 8 = 4,
| где: | K - число независимых контуров в механизме; pi - число КП в механизме; n - число подвижных звеньев в механизме. |
Для решения задач синтеза и анализа сложных рычажных механизмов профессором Петербургского университета Ассуром Л.В. была предложена оригинальная структурная классификация. По этой классификации механизмы не имеющие избыточных связей и местных подвижностей состоят из первичных механизмов и структурных групп Ассура (см. рис. 2.6).
 |
| Рис. 2.6 |
Под первичным механизмом понимают механизм, состоящий из двух звеньев (одно из которых неподвижное) образующих кинематическую пару с одной Wпм=1 или несколькими Wпм = 1 подвижностями.
Примеры первичных механизмов даны на рис. 2.7.
 |
| Рис. 2.7 |
Структурной группой Ассура (или гуппой нулевой подвижности) называется кинематическая цепь, образованная только подвижными звеньями механизма, подвижность которой (на плоскости и в пространстве) равна нулю (Wгр = 0).
Конечные звенья групп Ассура, входящие в две кинематические пары, из которых одна имеет свободный элемент звена, называются поводками. Группы могут быть различной степени сложности. Структурные группы Ассура делятся на классы в зависимости от числа звеньев, образующих группу, числа поводков в группе, числа замкнутых контуров внутри группы. В пределах класса (по Ассуру) группы подразделяются по числу поводков на порядки (порядок группы равен числу ее поводков). Механизмы классифицируются по степени сложности групп входящих в их состав. Класс и проядок механизма определяется классом и порядком наиболее сложной из входящих в него групп. Особенность структурных групп Ассура - их статическая определимость. Если группу Ассура свободными элементами звеньев присоединить к стойке, то образуется статически определимая ферма. Используя группы Ассура удобно проводить структурный, кинематический и силовой анализ механизмов. Наиболее широко применяются простые рычажные механизмы, состоящие из групп Ассура 1-го класса 2-го порядка. Число разновидностей таких групп для плоских механизмов с низшими парами невелико, их всего пять (см. рис. 2.8)
 |
| Рис. 2.8 |
Для этих групп разработаны типовые методы структурного, кинематического и силового анализа (см. например, алгоритмы в [6] и программу DIADA). При структурном синтезе механизма по Ассуру (рис.2.6) к выбранным первичным механизмам с заданной подвижностью W0 последовательно присоединяются структурные группы c нулевой подвижностью. Полученный таким образом механизм обладает рациональной структурой, т.е. не содержит избыточных связей и подвижностей. Структурному анализу по Ассуру можно подвергать только механизмы не содержащие избыточных связей и подвижностей.
Поэтому перед проведением структурного анализа необходимо устранить избыточные связи и выявить местные подвижности. Затем необходимо выбрать первичные механизмы и, начиная со звеньев наиболее удаленных от первичных, выделять из состава механизма структурные группы нулевой подвижности (схема на рис. 2.6). При этом необходимо следить, чтобы звенья, остающиеся в механизме, не теряли связи с первичными механизмами.
Несколько слов о историческом развитии классификации Ассура. В диссертационной работе Ассур разработал структурную классификацию для плоских рычажных шарнирных механизмов (т.е. для механизмов только с вращательными КП). В дальнейшем Артоболевский И.И. усовершенствовал и дополнил эту классификацию, распространив ее на плоские механизмы и с поступательными КП. При этом были изменены и принципы классификации. В плоских механизмах группами являются кинематические цепи с низшими парами, которые удовлетворяют условию Wгр = 3*nгр - 2*p1 = 0. Решения этого уравнения в целых числах определяют параметры групп Ассура. Эти параметры, а также классы простейших групп Ассура по Ассуру и по Артоболевскому приведены в таблице 2.2.
| Класс и порядок по Ассуру | 1 кл. 2 пор. | 1 кл. 3 пор. | |
| Число звеньев группы nгр | 2 | 4 | и т. д. |
| Число кинематических пар p1 | 3 | 6 | |
| Класс и порядок по Артоболевскому | 2 кл. 2 пор. | 3 кл. 3 пор. |
Проведем структурный анализ плоского механизма, схема которого приведена на рис. 2.4, и представим его в виде совокупности первичного механизма и структурных групп Ассура. Результаты структурного анализа изображены на рис. 2.9. Для рассматриваемого механизма структурный анализ можно проводить только для плоской модели, так как она не содержит избыточных связей. Механизм состоит из четырех структурных групп: двух рычажных двухповодковых ( группы звеньев 5-6 и 4-5) и двух групп с высшими парами одна из которых содержит только одно звено 2, вторая - два звена 7 и 8.
Звено 7 и пара T введены в структуру механизма с целью замены трения скольжения трением качения, т.е. они обеспечивают местную подвижность ролика 7. За вычетом этой подвижности группа 7-8 имеет нулевую подвижность и является группой Ассура (точнее группой нулевой подвижности). Механизм имеет одну основную подвижность и, следовательно, один первичный механизм, состоящий из звеньев 1 и 0. Если рассмотреть полученные структурные группы как пространственные, то они не будут группами нулевой подвижности ибо обладают избыточными связями. Чтобы преобразить их в группы с нулевой подвижностью необходимо снизить классы кинематических пар, не допуская при этом возникновения местных подвижностей. При переходе от анализа механизма на плоскости к анализу в пространстве изменяются классы пар: одноподвижная поступательная КП D изменяется на двухподвижную цилиндрическую, двухподвижные высшие P и K на четырехподвижные. Далее по группам классы пар изменялись так:
| группа звеньев 5-6 |  | |
| группа звеньев 3-4 |  | |
| группа звеньев 7-8 звено 2 |
 |
 |
| Рис. 2.9 |
После таких изменений классов КП подвижность механизма
Wпр = 6*8 - (3*1 + 4*4 + 5*5 + 1*2) = 48 - 46 = 2,
где одна подвижность - основная, а вторая - местная.
В данном случае для устранения избыточных связей мы воспользовались способом снижения классов КП. Другой способ - введение в механизм дополнительных звеньев и КП. В заключение необходимо отметить, что устранять избыточные связи нужно не всегда. Многоподвижные КП сложнее и дороже в изготовлении, механизмы с такими парами часто обладают меньшей жесткостью и точностью, чем механизмы с одноподвижными КП.
Классификация зубчатых передач
|
Краткое содержание: Классификация зубчатых передач. Понятие о блокирующем контуре. Качественные показатели для эвольвентной передачи. Коэффициент перекрытия. Коэффициент формы зуба. Коэффициент удельного давления. Коэффициент удельного скольжения Оптимальный геометрический синтез зубчатой передачи. Программное обеспечение САПР зубчатых передач. Косозубые цилиндрические эвольвентные передачи и особенности их расчета. Коэффициент осевого перекрытия.
Классификация зубчатых передач
Цилиндрические эвольвентные зубчатые передачи в зависимости от величины воспринимаемого смещения классифицируются следующим образом.
 |
нулевые или равносмещенные (составленные из зубчатых колес без смещения или с равными, но противоположными по знаку смещениями) x1 = x2 = 0 или x1 = - x2 , D1 = D2 = 0 или D1 = - D2 , yЧm = 0, y = 0, aw= a = r1 + r2 , aw = a ;
положительные (составленные из колес с положительными смещениями или когда положительное смещение одного колеса больше отрицательного смещения другого) x1 > 0, x2 > 0 или x1 > | - x2 | , D1 > 0, D2 > 0 или D1 > | - D2 | , yЧm > 0, y > 0, aw> a , aw > a ; отрицательные (составленные из колес с отрицательными смещениями или когда отрицательное смещение одного колеса больше положительного смещения другого) x1 < , x2 < 0 или x1 < - x2 | , D1 < 0, D2 < 0 или D1 < | - D2 | , yЧm < 0, y < 0, aw< a , aw < a . |
Понятие о блокирующем контуре зубчатой передачи
При проектировании зубчатой передачи необходимо решить несколько задач: выбрать тип зубчатого механизма, его передаточное отношение и числа зубьев колес; провести проектный прочностной расчет механизма и определить величину межосевого расстояния или модуль зубчатых колес( модуль зубчатых колес округляется до ближайшей величины из стандартного ряда модулей ); · провести геометрический расчет зубчатой передачи для выбранных коэффициентов смещения исходного контура, которые обеспечивают исключение подрезания, срезания и заострения зубьев колес и благоприятное или оптимальное сочетание качественных показателей зубчатой передачи.Для эвольвентных зубчатых передач, по предложению М.Б.Громана, область сочетаний коэффициентов смещений зубчатых колес x1 и x2, удовлетворяющих ограничениям по срезанию в станочном зацеплении, заострению, заклиниванию в зацеплении эвольвент и на переходных кривых, по допустимым минимальным или максимальным значениям качественных показателей, называют блокирующим контуром (рис.13.2).
Границы блокирующего контура отсекают те значения коэффициентов смещению которые недопустимы по указанным условиям. Значения, расположенные внутри контура, допустимы, но каждой паре коэффициентов смещения соответствует свое сочетание качественных показателей. Для выбора коэффициентов смещения на блокирующий контур наносятся изолинии качественных показателей, с использованием которых внутри контура выбираются коэффициенты смещения с оптимальным сочетанием качественных показателей. И.И.Болотовским и его сотрудниками созданы справочники, которые содержат блокирующие контуры для большого числа зубчатых передач. Построение блокирующего контура является трудоемкой вычислительной задачей и требует значительных затрат даже при применении ЭВМ. В настоящее время, с ростом производительности компьютеров, появляется возможность геометрического синтеза оптимальных зубчатых передач без предварительного построения блокирующего контура.
 |
На рис. 13.2 ограничивающие линии блокирующего контура: 1 - коэффициент торцевого перекрытия ea =1; 2 - толщина зуба колеса z1 по окружности вершин sa1 = 0; 3 - допустимое подрезание колеса z2 ; 4 - допустимое подрезание колеса z1 ; 5 - интерференция или заклинивание с переходной кривой колеса z2. Линии качественных показателей: 6 - линия sa2 = 0.25m; 7 - линия sa2 = 0.4m; 8 - линия выравненных удельных скольжений l1=l2; 9 - линия sa1 = 0.4m; 10 - линия sa1 = 0.25m; 11 - линия x2 = x2min ; 12 - линия x1 = x1min ; 13 - линия ea = 1.2. |
К качественным показателям цилиндрической эвольвентной зубчатой передачи относятся:
коэффициент торцевого перекрытия коэффициент полезного действия коэффициент удельного скольжения коэффициент удельного давления коэффициент формы зуба Рассмотрим эти коэффициенты подробнее (исключив из рассмотрения коэффициент полезного действия, как величину характеризующую реальные, а не рассматриваемые нами идеализированные механизмы). Коэффициент торцевого перекрытия
Коэффициентом перекрытия eg называется величина отношения угла перекрытия зубчатого колеса к его угловому шагу, где под углом перекрытия понимают угол на который поворачивается колесо за время зацепления одной пары зубьев. Для цилиндрических колес различают полное eg, торцевое ea и осевое перекрытие:

где осевое перекрытие имеется только в косозубых передачах.

где,


Коэффициент перекрытия определяет величину зоны двухпарного контакта, когда одновременно зацепляются два последовательно расположенных зуба. Так как до окончания зацепления одной пары зубьев, следующая пара должна войти в контакт, нельзя допускать в прямозубых передачах

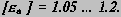


Коэффициент формы зуба Геометрическая форма зуба в значительной мере определяет показатели его как изгибной, так и контактной прочности. Оценка влияния геометрии зуба на изгибную прочность осуществляется коэффициентом формы зуба Y. Этот коэффициент определяется через параметры балки параболиче-
 |
ского сечения (балки равного сопротивления изгибу), которая вписывается в контур зуба так, чтобы вершина параболы располагалась в точке пересечения оси зуба и нормали к профилю в вершине, а ветви касались профиля зуба у основания ( см. схему на рис. 13.4). где Sp - толщина зуба по хорде на окружности, проходящей через точки касания параболы и профиля зуба, l - высота от вершины параболы до хорды Sp . |
Коэффициент удельного давления Для характеристики влияния геометрической формы зуба на контактную прочность используется коэффициент удельного давления



где - радиусы кривизны профилей в контактной точке, знак + относится к внешнему зацеплению, - к внутреннему. Чтобы коэффициент давления характеризовал контактное напряжение не-зависимо от абсолютных размеров зуба, которые определяются модулем, введено понятие удельного давления как отношения модуля к приведенному радиусу кривизны

Для цилиндрической прямозубой эвольвентной передачи:

Тогда для внешнего зацепления: при контакте в точке В2 (на выходе зубьев из зацепления) :

при контакте в точке В1 (на входе зубьев в зацепление)

при контакте в полюсе точке Р:

Коэффициент удельного скольжения. Как показано выше, скорость скольжения в точке контакта профилей высшей пары определяется следующим выражением :

где l кр - расстояние от точки контакта до полюса, знак + для внешнего зацепления , для внутреннего. Величина износа активных частей профилей в высшей паре в значительной степени зависит от их относительного скольжения и от скорости этого скольжения. Для оценки скольжения при геометрических расчетах зубчатых передач пользуются коэффициентом удельного скольжения

где Vtki - проекция скорости контактной точки звена i на контактную нормаль. Из схемы эвольвентного зацепления ( [ 1 ] стр.105 рис. 86 )

после подстановки и преобразований для колеса z1 при контакте в точке В2 (на выходе зубьев из зацепления)

для колеса z2 при контакте в точке В1 (на входе зубьев в зацепление)

Графики изменения коэффициентов удельного давления и удельного скольжения по линии зацепления зубчатых колес.

Оптимальный геометрический синтез зубчатой передачи. Оптимальный геометрический синтез зубчатой передачи проводится аналогично оптимальному метрическому синтезу рычажных механизмов, но с использованием других ограничений и других качественных показателей.
Среди качественных показателей необходимо различать противоречивые и непротиворечивые. Так с увеличением смещений удельное давление и коэффициент формы зуба изменяются в желаемом направлении, а коэффициент торцевого перекрытия и толщины зубьев по окружностям вершин уменьшаются, что, при упрощенном рассмотрении, можно считать нежелательным. Критерии или качественные показатели, которые при принятом изменении параметров изменяются в желаемом направлении считаются непротиворечивыми (так как не противоречат друг другу), те критерии, которые при этом изменяются нежелательным образом, называются противоречивыми. При наличии противоречивых критериев эффективным методом поиска оптимума является метод "минимизации уступок". При этом методе вначале проводится оптимизация по каждому из рассматриваемых критериев, определяются значения критериев в оптимальных точках и ищутся значения параметров при которых отклонения каждого критерия от его оптимального значения будут минимальны. Необходимо отметить, что возможности параметрической оптимизации достаточно скромны. Обычно в среднем можно получить улучшение по каждому из показателей не более 10 - 20%. Более существенных результатов можно достичь при переходе к другой схеме или другому типу механизма. Кроме того при геометрическом синтезе зубчатой передаче сложно ориентироваться в сочетании качественных показателей. При анализе скольжения необходимо учитывать, что создание устойчивой масляной пленки в зоне контакта возможно при определенных значениях скорости скольжения. В полюсе зацепления скорость скольжения равна нулю и при прохождении полюса эта скорость изменяет свой знак. Поэтому в зубчатых передачах при дозаполюсном зацеплении в зоне близкой к полюсу происходит нарушение масляной пленки, что приводит к повышенному износу в этой зоне за счет контактного выкрашивания - питтинга. С этих позиций предпочтительными оказываются передачи с большими смещениями с до или заполюсным зацеплением, в которых скорость скольжения направлена в одну сторону, не имеет нулевых значений, поэтому условия для формирования масляной пленки более благоприятны.
Программное обеспечение САПР зубчатых передач. В 70 - е годы были разработаны и приняты ГОСТ на терминологию, прочностные и геометрические расчеты эвольвентных зубчатых передач. Поэтому программное обеспечение САПР зубчатых передач по всем направлениям проводится по расчетным формулам и алгоритмам рекомендуемым ГОСТ. В ГОСТ предусмотрены два вида расчета геометрии:
по стандартному радиальному зазору в передаче; по стандартной высоте зуба. При изучении курса ТММ в МВТУ им. Баумана принят метод расчета по стандартной величине радиального зазора. Существующее на кафедре программное обеспечение разработано для этого вида расчета и обеспечивает расчет геометрии внешнего зацепления при фиксированном значении x2 = 0.5 и изменении x1 в диапазоне от 0 до 1.4 с шагом 0.1. При выполнении курсового проекта по ТММ на основании этого расчета строятся графики качественных показателей, определяется область допустимых решений для коэффициента x1 и выбор этого по оптимальному сочетанию качественных показателей. На рис. 13.6 приведен пример графика. При принятых допустимых значениях
[Ea] =1.1. и [Sa/m]=0.3
ограничения на выбор коэффициента смещения x1 :
по подрезанию X1min = 0.24 ;
по заострению колеса z1 : X1maxsa = 1.24;
по торцевому перекрытию :X1maxea = 0.84.
Таким образом, область допустимых значений (ОДЗ), в которой можно выбирать значение x1 0.24 > x1 > 0.84. этой области выбирается то значение x1, которое обеспечивает наилучшее сочетание качественных показателей. Часто выбор коэффициента производят по рекомендациям ГОСТ. Для рассматриваемого случая силовой зубчатой передачи с числами зубьев z1 = 14 и z2 = 22
x1 = x2 = 0.5 .

Косозубые цилиндрические эвольвентные передачи и особенности их расчета. Косозубыми называются цилиндрические эвольвентные зубчатые передачи, боковая поверхность зуба которой образована наклонной прямой лежащей в производящей плоскости и образующей с линией касания с основным цилиндром угол bb ( см. схему на рис. 13.7). При этом эвольвентами основной окружности радиуса rb будут кривые лежащие в торцевой плоскости.
Поэтому расчет геометрии цилиндрической косозубой передачи проводится по приведенным выше формулам для торцевого сечения. Для передачи с косыми зубьями нужно ввести несколько новых параметров:

осевой шаг - расстояние между одноименными линиями соседних винтовых зубьев по линии пересечения плоскости осевого сечения зубчатого колеса с делительной, начальной или другой соосной поверхностью. На рис. 13.7 справа изображены развертки делительного и начального цилиндров косозубого колеса. Из этой схемы:


 |
Из схемы, изображенной на рис. 13.8 |
 |
 |

Коэффициент осевого перекрытия. В косозубых передачах величина коэффициента перекрытия увеличивается на величину торцевого перекрытия, которое (рис. 13.8) равно:

где





Кулачковые механизмы
|
Краткое содержание:
[Назначение и область применения]
[Классификация кулачковых механизмов]
[Основные параметры кулачковых механизмов]
[Структура кулачкового механизма]
[Кинематический анализ кулачкового механизма]
[Синтез кулачкового механизма]
[Этапы синтеза]
[Постановка задачи метрического синтеза]
[Алгоритм проектирования кулачкового механизма по допустимому углу давления]
[Проверка результатов синтеза по диаграмме углов давления]
Кулачковые механизмы:
Кулачковые механизмы:
Кулачковым называется трехзвенный механизм с высшей кинематической парой входное звено которого называется кулачком, а выходное - толкателем (или коромыслом). Часто для замены в высшей паре трения скольжения трением качения и уменьшения износа, как кулачка, так и толкателя, в схему механизма включают дополнительное звено – ролик и вращательную кинематическую пару. Подвижность в этой кинематической паре не изменяет передаточных функций механизма и является местной подвижностью.
Назначение и область применения:
Кулачковые механизмы предназначены для преобразования вращательного или поступательного движения кулачка в возвратно-вращательное или возвратно-поступательное движение толкателя. При этом в механизме с двумя подвижными звеньями можно реализовать преобразование движения по сложному закону. Важным преимуществом кулачковых механизмов является возможность обеспечения точных выстоев выходного звена. Это преимущество определило их широкое применение в простейших устройствах цикловой автоматики и в механических счетно-решающих устройствах (арифмометры, календарные механизмы). Кулачковые механизмы можно разделить на две группы. Механизмы первой обеспечивают перемещение толкателя по заданному закону движения. Механизмы второй группы обеспечивают только заданное максимальное перемещение выходного звена – ход толкателя. При этом закон, по которому осуществляется это перемещение, выбирается из набора типовых законов движения в зависимости от условий эксплуатации и технологии изготовления.
Классификация кулачковых механизмов:
Кулачковые механизмы классифицируются по следующим признакам:
по расположению звеньев в пространстве
пространственные плоские
по движению кулачка
вращательное поступательное винтовое
по движению выходного звена
возвратно-поступательное ( с толкателем) возвратно-вращательное ( с коромыслом)
по наличию ролика
с роликом без ролика
по виду кулачка
дисковый (плоский) цилиндрический коноид (сложный пространственный)
по форме рабочей поверхности выходного звена
плоская заостренная цилиндрическая сферическая эвольвентная
по способу замыкания элементов высшей пары
силовое геометрическое При силовом замыкании удаление толкателя осуществляется воздействием контактной поверхности кулачка на толкатель (ведущее звено – кулачок, ведомое – толкатель). Движение толкателя при сближении осуществляется за счет силы упругости пружины или силы веса толкателя, при этом кулачок не является ведущим звеном. При геометрическом замыкании движение толкателя при удалении осуществляется воздействием наружной рабочей поверхности кулачка на толкатель, при сближении – воздействием внутренней рабочей поверхности кулачка на толкатель. На обеих фазах движения кулачок ведущее звено, толкатель – ведомое.
Рис. 17.1
 |
 |
|
Кулачковый механизм с силовым замыканием высшей пары |
Кулачковый механизм с геометрическим замыканием высшей пары |
Большинство кулачковых механизмов относится к цикловым механизмам с периодом цикла равным 2p. В цикле движения толкателя в общем случае можно выделить четыре фазы: удаления, дальнего стояния (или выстоя), сближения и ближнего стояния.
В соответствии с этим, углы поворота кулачка или фазовые углы делятся на: угол удаления jy угол дальнего выстоя jдв угол сближения jс угол ближнего выстоя jбв. Сумма трех углов образует угол jраб = dраб , который называется рабочим углом.
jраб = dраб = jу + jдв + jс . Кулачок механизма характеризуется двумя профилями: центровым (или теоретическим) и конструктивным.
Под конструктивным понимается наружный рабочий профиль кулачка. Теоретическим или центровым называется профиль, который в системе координат кулачка описывает центр ролика (или скругления рабочего профиля толкателя) при движении ролика по конструктивному профилю кулачка. Фазовым называется угол поворота кулачка. Профильным углом di называется угловая координата текущей рабочей точки теоретического профиля, соответствующая текущему фазовому углу ji.
В общем случае фазовый угол не равен профильному ji№di.
На рис. 17.2 изображена схема плоского кулачкового механизма с двумя видами выходного звена: внеосным с поступательным движением и качающимся (с возвратно-вращательным движением). На этой схеме указаны основные параметры плоских кулачковых механизмов. Рис. 17.2

| SAi и SВi | - текущие значения перемещения центров роликов |
| j40 | - начальная угловая координата коромысла |
| j4 | - текущее угловое перемещение коромысла |
| hAmax | - максимальное перемещение центра ролика |
| r0 | - радиус начальной шайбы центрового профиля кулачка |
| r | - радиус начальной шайбы конструктивного профиля кулачка |
| rp | - радиус ролика (скругления рабочего участка толкателя) |
| Ji | - текущее значение угла давления |
| aw | - межосевое (межцентровое) расстояние |
| e | - внеосность (эксцентриситет) |
где ri - радиус-вектор текущей точки теоретического или центрового профиля кулачка.
Структура кулачковых механизмов: Рис. 17.3

| Wпл = 3Чn - 2Чpн - 1Чpвп | |
|
n = 3, pн = 3, pвп = 1, Wпл = 3Ч3 - 2Ч3 - 1Ч1 = 2 = 1 + 1 W0 = 1, Wм = 1 |
n = 2, pн = 2, pвп = 1, Wпл = 3Ч2 - 2Ч2 - 1Ч1 = 1 ; W0 = 1 ; Wм = 0. |
Кинематический анализ кулачкового механизма:
Кинематический анализ кулачкового механизма может быть проведен любым из описанных выше методов. При исследовании кулачковых механизмов с типовым законом движения выходного звена наиболее часто применяется метод кинематических диаграмм. Для применения этого метода необходимо определить одну из кинематических диаграмм. Так как при кинематическом анализе кулачковый механизм задан, то известна его кинематическая схема и форма конструктивного профиля кулачка. Построение диаграммы перемещений проводится в следующей последовательности (для механизма с внеосным поступательно движущимся толкателем): строится, касательно к конструктивному профилю кулачка, семейство окружностей с радиусом, равным радиусу ролика; соединяются центры окружностей этого семейства плавной кривой и получается центровой или теоретический профиль кулачка в полученный центровой профиль вписываются окружности радиусов r0 и r0 +hAmax,определяется величина эксцентриситета е по величине участков, не совпадающих с дугами окружностей радиусов r0 и r0 +hAmax , определяются фазовые углы jраб , jу , jдв и jс дуга окружности r, соответствующая рабочему фазовому углу, разбивается на несколько дискретных участков; через точки разбиения проводятся касательно к окружности радиуса эксцентриситета прямые линии (эти линии соответствуют положениям оси толкателя в его движении относительно кулачка) на этих прямых измеряются отрезки расположенные между центровым профилем и окружностью радиуса r0 ; эти отрезки соответствуют перемещениям центра ролика толкателя SВi
по полученным перемещениям SВiстроится диаграмма функции положения центра ролика толкателяSВi= f(j1) Рис.17.4

Синтез кулачкового механизма. Этапы синтеза:
При синтезе кулачкового механизма, как и при синтезе любого механизма, решается ряд задач из которых в курсе ТММ рассматриваются две:
выбор структурной схемы и определение основных размеров звеньев механизма (включая профиль кулачка). Первый этап синтеза – структурный. Структурная схема определяет число звеньев механизма; число, вид и подвижность кинематических пар; число избыточных связей и местных подвижностей. При структурном синтезе необходимо обосновать введение в схему механизма каждой избыточной связи и местной подвижности. Определяющими условиями при выборе структурной схемы являются: заданный вид преобразования движения, расположение осей входного и выходного звеньев. Входное движение в механизме преобразуется в выходное, например, вращательное во вращательное, вращательное в поступательное и т.п. Если оси параллельны, то выбирается плоская схема механизма. При пересекающихся или перекрещивающихся осях необходимо использовать пространственную схему. В кинематических механизмах нагрузки малы, поэтому можно использовать толкатели с заостренным наконечником. В силовых механизмах для повышения долговечности и уменьшения износа в схему механизма вводят ролик или увеличивают приведенный радиус кривизны контактирующих поверхностей высшей пары. Второй этап синтеза – метрический. На этом этапе определяются основные размеры звеньев механизма, которые обеспечивают заданный закон преобразования движения в механизме или заданную передаточную функцию. Как отмечалось выше, передаточная функция является чисто геометрической характеристикой механизма, а, следовательно, задача метрического синтеза чисто геометрическая задача, независящая от времени или скоростей. Основные критерии, которыми руководствуется проектировщик, при решении задач метрического синтеза: минимизация габаритов, а , следовательно, и массы; минимизация угла давления в вышей паре; получение технологичной формы профиля кулачка.
Постановка задачи метрического синтеза: Дано:
Структурная схема механизма; закон движения выходного звена SB=f(j1)
или его параметры – hB , jраб = jу + jдв + jс , допустимый угол давления - |J|
Дополнительная информация: радиус ролика rр , диаметр кулачкового вала dв , эксцентриситет е(для механизма с толкателем движущимся поступательно), межосевое расстояние awи длина коромысла lBC(для механизма с возвратно-вращательным движением выходного звена). Определить:
радиус начальной шайбы кулачка r0 ; радиус ролика r0 ; координаты центрового и конструктивного профиля кулачка ri = f(di)
и, если не задано, то эксцентриситет е и межосевое расстояние aw.
Алгоритм проектирования кулачкового механизма по допустимому углу давления: 1. Определение закона движения . Если в задании на проектирование не дан закон движения , то конструктор должен выбрать его и набора типовых Таблица 17.1
|
№ п.п. |
Типовой закон движения |
Параметры закона движения | ||||
| 1. |
 |
с жесткими ударами
| ||||
| 2. |
 |
с мягкими ударами aq1№aq2; jур№jур; aq1Чjур = aq2Чjут или aq1 = aq2; jур = jур; aq1Чjур = aq2Чjут | ||||
| 3. |
 |
с мягкими ударами aq1 № aq2; jур № jут; aq3 № aq4 ; (aq1+aq2)Ч jур = =(aq3+aq4)Чjут | ||||
| 4. |
 |
с мягкими ударами aq1 № aq2; jур№jут; 0.5Ч aq1Чjур= 0.5Ч aq2Чjут | ||||
| 5. |
 |
безударный aq1 № aq2; jур№jут; 0.5Ч aq1Чjур= 0.5Ч aq2Чjут | ||||
| 6. |
 |
безударный aq1 № aq2; jур№jут ;  |
Размеры кулачкового механизма определяются с учетом допустимого угла давления в высшей паре. При этом используется условие, доказанное выше, и названное нами вторым следствием основной теоремы зацепления. Формулировка синтеза: Если на продолжении луча, проведенного из точки О2 через точку K, отложить от точки K отрезок длиной lKD = VK2 / w1 = VqK2 и через конец этого отрезка провести прямую параллельную контактной нормали, то эта прямая пройдет через центр вращения ведущего звена точку О1 . Условие, которому должно удовлетворять положение центра вращения кулачка О1, согласно этой теореме: углы давления на фазе удаления во всех точках профиля должны быть меньше допустимого значения. Поэтому графически область расположения точки О1 может быть определена семейством прямых проведенных под допустимым углом давления к вектору возможной скорости точки центрового профиля, принадлежащей толкателю. Графическая интерпретация вышесказанного для толкателя и коромысла дана на рис. 17.5. На фазе удаления строится диаграмма зависимости SB=f(j1). Так как при коромысле точка В движется по дуге окружности радиуса lBC , то для механизма с коромыслом диаграмма строится в криволинейных координатах. Все построения на схеме, проводятся в одном масштабе, то есть ml= mVq= mS. Рис.17.5

| Механизм с толкателем | Механизм с коромыслом |
Радиус начальной шайбы кулачка r1aw при заданном межосевом расстоянии aw, определяется точкой О1aw , пересечения дуги радиуса aw с соответствующей границей области. Обычно кулачок вращается только в одном направлении, но при проведении ремонтных работ желательно иметь возможность вращения кулачка в противо-положном направлении, то есть обеспечить возможность реверсивного движения кулачкового вала. При изменении направления движения, фазы удаления и сближения, меняются местами. Поэтому для выбора радиуса кулачка, движуще-гося реверсивно, необходимо учитывать две возможных фазы удаления, то есть строить две диаграммы SВ= f(j1) для каждого из возможных направлений дви-жения. Выбор радиуса и связанных с ним размеров реверсивного кулачкового механизма проиллюстрирован схемами на рис. 17.6. На этом рисунке: r1 - минимальный радиус начальной шайбы кулачка;
r1е - радиус начальной шайбы при заданном эксцентриситете;
r1aw - радиус начальной шайбы при заданном межосевом расстоянии;
aw0 – межосевое расстояние при минимальном радиусе. Рис.17.6
 Механизм с толкателем |
 Механизм с коромыслом |
В кулачке, из- за сложной конфигурации рабочей поверхности, это обеспечить сложнее. Поэтому обычно радиус ролика rр меньше радиуса начальной шайбы конструктивного профиля r и удовлетворяет соотношению rр < 0.4Ч r0
,где r0 - радиус начальной шайбы теоретического профиля кулачка. Выполнение этого соотношения обеспечивает примерно равную контактную прочность как для кулачка, так и для ролика. Ролик обладает большей контактной прочностью, но так как его радиус меньше, то он вращается с большей скоростью и рабочие точки его поверхности участвуют в большем числе контактов. Конструктивный профиль кулачка не должен быть заостренным или срезанным. Поэтому на выбор радиуса ролика накладывается ограничение
rр <0.7 Чrmin , где rmin - минимальный радиус кривизны теоретического профиля кулачка (см. рис. 17.7). Рис.17.7

Рекомендуется выбирать радиус ролика из стандартного ряда диаметров в диапазоне rp = (0.2 … 0.35) Ч r0 . При этом необходимо учитывать, что увеличение радиуса ролика увеличивает габариты и массу толкателя, ухудшает динамические характеристики механизма (уменьшает его собственную частоту). Уменьшение радиуса ролика увеличивает габариты кулачка и его массу; частота вращения ролика увеличивается, его долговечность снижается. При выборе радиуса скругления рабочего участка толкателя подход к решению задачи несколько иной. Так как в этом случае нет местной подвижности, заменяющей скольжение качением, то на толкателе имеется очень небольшой рабочий участок, точки которого скользят относительно рабочей поверхности кулачка, то есть износ поверхности толкателя более интенсивный. Увеличение радиуса скругления не увеличивает габаритов и массы толкателя, а размеры конструктивного профиля кулачка уменьшаются. Поэтому этот радиус можно выбирать достаточно большим. Часто применяются толкатели с плоской рабочей поверхностью кулачка (радиус скругления равен бесконечности). В этом случае угол давления в высшей паре при поступательном движении толкателя есть величина постоянная и равная углу между нормалью к плоскости толкателя и вектором скорости его движения на фазе удаления.
Определение размеров по углу давления при этом невозможно. Радиус кулачка при этом определяют по контактным напряжениям, а форму профиля проверяют по условию выпуклости (1). 3. Построение центрового и конструктивного профилей кулачка. 3.1. Для кулачкового механизма с внеосным толкателем.: Построение профилей кулачка проводится в следующей последовательности: выбирается масштаб построения ml,мм/м из произвольного центра проводятся в масштабе окружности с радиусами r0и е. из произвольной точки на окружности r0 в направлении - j1откладываeтся рабочий угол, угол делятся на n интервалов. из каждой точки деления касательно к окружности радиусом е проводятся прямые. на этих прямых от точки пересечения с окружностью r0 откладываются в масштабе mlсоответствующие перемещения толкателя SВi. полученные точки соединяются плавной кривой , образуя центровой профиль кулачка. проводятся из произвольных точек выбранных равномерно по центровому профилю кулачка дуги окружностей радиуса rp. конструктивный профиль кулачка получаем как огибающую к множеству положений ролика толкателя. 3.1. Для кулачкового механизма с коромыслом: Построение профилей кулачка проводится в следующей последовательности: выбирается масштаб построения ml,мм/м, из произвольного центра проводятся в масштабе окружности с радиусами r0и aw,
из произвольной точки на окружности aw в направлении - j1откладываeтся рабочий угол, угол делится на n интервалов, из каждой точки деления радиусом lBC проводятся дуги.
Рис.17.8


на этих дугах от точки пересечения с окружностью r0 откладываются в масштабе mlсоответствующие перемещения толкателя SВi. полученные точки соединяются плавной кривой, образуя центровой профиль кулачка. проводятся из произвольных точек выбранных равномерно по центровому профилю кулачка дуги окружностей радиуса rр. конструктивный профиль кулачка получаем как огибающую к множеству положений ролика толкателя.
Проверка результатов синтеза по диаграмме углов давления. 1. Построение диаграммы углов давления для механизма с геометрическим замыканием высшей пары. Как отмечено выше, ведущим звено в течение всего цикла кулачок является только в механизме с геометрическим замыканием.
Причем на фазе удаления рабочим является либо второй профиль кулачка (рис.17.1), либо другой участок поверхности толкателя, либо второй ролик. Поэтому на диаграмме угла давления необходимо четко различать фазы удаления и сближения. На рис. 17.10 дан пример диаграммы угла давления для механизма с коромыслом при геометрическом замыкании. При синтезе эта диаграмма позволяет проверить какие углы давления обеспечивают выбранные размеры механизма и полученный профиль кулачка. Угол давления определяем как острый угол между нормалью к профилю ( прямая соединяющая точку контакта с центром ролика ) и направлением перемещения точки В толкателя. Рис.17.10



Метрический синтез типовых рычажных механизмов
|
Краткое содержание: Метрический синтез типовых рычажных механизмов. Структурные схемы простейших типовых механизмов. Цель и задачи метрического синтеза механизмов. Методы метрического синтеза механизмов. Условия проворачиваемости звеньев механизма. Понятие о коэффициенте неравномерности средней скорости и о угле давления в рычажном механизме. Частные задачи синтеза: четырехшарнирный механизм - синтез по kv и синтез по двум положениям выходного звена; кривошипно-ползунный механизм - синтез по kv, по средней скорости ползуна, по двум положениям выходного звена; кулисный механизм - по рабочему перемещению выходного звена (для четырехзвенного механизма), по коэффициенту kv (для шестизвенного механизма). Оптимальный синтез рычажных механизмов. Синтез механизма по заданной функции положения.
Метрический синтез типовых рычажных механизмов.
Под метрическим синтезом или проектированием механизмов понимают определение линейных размеров и угловых положений звеньев по условиям рабочих положений и перемещений выходного звена. К решению задач метрического синтез приступают после определения структуры механизма - выбора его структурной схемы. В нашем курсе рассматриваются только простые типовые четырех- или шестизвеные рычажные механизмы.
Структурные схемы простейших типовых механизмов.
Цель и задачи метрического синтеза механизмов.
Цель метрического синтеза механизма - определение размеров механизма и положений его входного звена наилучшим образом удовлетворяющих заданным условиям и обеспечивающих наилучшее (оптимальное) сочетание качественных показателей.
Из множества возможных задач решаемых при метрическом синтезе наиболее распространены:
синтез по нескольким заданным положениям выходного звена (задача позиционирования), когда не важно по какому закону происходит переход из одного положения в другое; синтез по заданному закону движения выходного звена (по функции положения, по первой или второй передаточной функции); синтез по конкретным кинематическим параметрам: средней скорости выходного звена, коэффициенту неравномерности средней скорости; синтез по условиям передачи сил между звеньями механизма - по допустимому углу давления.В качестве ограничений или качественных показателей при метрическом синтезе механизмов используются:
условие проворачиваемости звеньев, т.е. обеспечение для входного и (или) выходного звеньев возможности поворота на угол более 360 градусов; допустимые углы давления, т.е. угол между вектором движущей силы, действующей с ведущего звена на ведомое, и вектором скорости точки ее приложения не должен превышать некоторых допустимых величин, чтобы исключить недопустимо большие величины реакций в КП, низкий КПД механизма, возможность его заклинивания (невозможность движения при любой величине движущей силы на входном звене); конструктивные ограничения на габариты механизма, т.е. размеры звеньев должны обеспечивать вписывание механизма в заданные габаритные размеры; точность обеспечения заданного закона движения или заданных положений звеньев механизма; другие условия и требования определяемые условиями функционирования и эксплуатации механизма. Методы метрического синтеза механизмов.
Как и общие методы проектирования, методы метрического синтеза условно делятся:
графоаналитические и аналитические методы прямого синтеза (разработаны для типовых и ряда специальных механизмов, частично рассмотрены ниже); синтез методами анализа: оптимальноепроектирование: Градиентные методы, метод случайного поиска, минимизация уступок, комбинированные методы, другие; автоматизирование проектирование. Условия проворачиваемости звеньев механизма.
Часто по условиям работы требуется, чтобы входное и (или) выходное звенья могли в процессе движения поворачиваться на угол более 360 градусов. Для обеспечения этого необходимо выполнить некоторые условия, которые накладываются на соотношение длин звеньев механизма.
Для четырехшарнирного механизма эти соотношения сформулированы в правиле или теореме Грасгофа:
Если сумма длин наибольшего и наименьшего звеньев меньше суммы двух остальных и стойкой является наименьшее звено, то механизм - двухкривошипный. Если неравенство выполняется, но стойкой является звено соединенное с наименьшим, то механизм - кривошипно-коромысловый. Во всех остальных случаях механизм - двухкоромысловый.
Математически это можно записать так:
при L1 > L2 > L3 > L4 , где Li присваивается значение длины звена, удовлетворяющей этому неравенству,
если L1 + L4 < L2 + L3 и L1 = l0 , то механизм двухкривошипный;
если L1 + L4 < L2 + L3 и L1 = l1 или L1 = l3 ,то механизм кривошипно-коромысловый; иначе механизм двухкоромысловый.
Для кривошипно-ползунного механизма условие существования кривошипа
l1 < l2 - | e | .
Если условие выполняется - механизм кривошипно-ползунный, нет - коромыслово-ползунный.
Понятие о коэффициенте неравномерности средней скорости и о угле давления в рычажном механизме.
1. Четырехшарнирный механизм.
На рис. 10.7 изображен четырехшарнирный механизм . К входному звену 1 этого механизма приложен движущий момент Мд , к выходному звену 3 -
момент сопротивления Мс3. На этапе проектирования массы и моменты инерции звеньев не Рис. 10.7 определены, поэтому движущая сила действующая на ведомое звено - реакция F32 направлена по линии ВС, скорость точки ее приложения на звене 3 - VC направлена в сторону w 3 перпендикулярно звену 3. Угол J 32 между векторами F32 и VC - угол давления во вращательной паре С. С увеличением этого угла тангенциальная составляющая силы Ft32, способствующая повороту звена 3 в направлении w 3, уменьшается , а нормальная Fn32, которая не влияет на движение, а только деформирует (сжимает) звено 3, увеличивается. То есть с увеличением угла давления условия передачи сил в КП ухудшаются. Так как в реальных КП всегда имеется трение, то при определенной величине угла давления в КП возможно самоторможение или заклинивание. Самоторможение или заклинивание - это такое состояние механизма, когда в результате возрастания углов давления в одной из КП , движение механизма становится невозможным при сколь угодно большом значении движущей силы. Часто для характеристики условий передачи сил пользуются коэффициентом возрастания усилий (без учета трения)
kJ = F32 / Ft32 = 1/ cos J 32 .
Коэффициентом неравномерности средней скорости kw называется отношение средней скорости выходного звена на обратном ходе w 3ср ох к средней скорости прямого хода w 3ср
где w 3ср ох = D j 3/tох ,
w 3ср пх = D j 3/tпх ,
tох и tпх - соответственно время обратного и время прямого хода.
При проектировании технологических машин, в которых нагрузка на выходном звене механизма на рабочем или прямом ходе намного больше нагрузки на холостом или обратном ходе, желательно, чтобы скорость выходного звена на прямом ходе была меньше, чем на обратном. С целью сокращения времени холостого хода, тоже необходимо увеличивать скорость при обратном ходе. Поэтому при метрическом синтезе механизма часто надо подбирать размеры звеньев обеспечивающие заданный коэффициент неравномерности средней скорости.
2. Кривошипно-ползунный механизм.
В кривошипно-ползунном механизме размеры механизма определяются углом давления в поступательной КП (рис.10.10).
при прямом ходе
sin J пх = ( l1 - e )/ l2 *sin [ J пх];
при обратном ходе
sin J ох = ( l1 + e )/ l2 *sin [ J ох].
Для поступательной КП : [ J пх] = 30; [ J ох] = 45° , тогда
l1 / l2 *( sin [ J ох] + sin [ J пх] )/ 2 ; l1 / l2 *( sin [ 45° ] + sin [ 30° ] )/ 2 ;
l1 / l2=0.6
Решение задач метрического синтеза для типовых четырехзвенных механизмов.
1. Проектирование по коэффициенту неравномерности средней скорости .
a)четырехшарнирный механизм
Дано: kw , HC, [ J ], j 30 , D j 3 , lDC
Определить: l i - ?
_____________________________________________________ от оси х откладывается начальное положение выходного звена и его рабочее перемещение точки С в начальном и в конечном положениях соединяют прямой и от перпендикуляров к этой прямой откладываем углы q и проводим лучи C'О определяем точку О - центр окружности r0 проходящей через точки C', и искомую точку A. Положение точки A на этой окружности определяется в зависимости от исходных данных:
в точке C от вектора скорости VC' откладывается угол давления J ? = [ J ], и проводится луч до пересечения с окружностью r0 в точке A ; как точка пересечения оси х с окружностью r0; как точка пересечения окружности r0 с окружностью радиуса l0 ( если величина l0 задана ). Затем по определенным таким образом размерам lAC' и lAC'' находим длины звеньев 1 и 2
lAC'= l2 + l1 , lAC'' = l2 - l1 ,
откуда
l1 = ( lAC'' - lAC' )/ 2 , l2 = ( lAC'' + lAC' )/ 2.
б)кривошипно-ползунный механизм;
Дано: kV, HC , [ J ]
Определить: l i - ?
____________________________________________________
от оси х откладывается рабочее перемещение выходного звена HC , точки С в начальном C'' и в конечном C' положениях соединяют прямой и от перпендикуляров к этой прямой откладываются углы q и проводятся лучи C' О и C''О и определяем точку О - центр окружности r0 проходящей через точки C', C'' и искомую точку A. Положение точки A на этой окружности определяется:
как точка пересечения луча AC'' с окружностью r0 (в точке C'' от вектора скорости VC'' откладывается угол давления J = [J ] и проводится луч AC'' до пересечения с окружностью r0 в точке A ); как точка пересечения прямой, проведенной на расстоянии заданного экспентриситета е и параллельной оси х, с окружностью r0 . Затем по размерам lAC' и lAC'' определяются длины звеньев 1 и 2
l1 = ( lAC' - lAC'' )/ 2 , l2 = ( lAC' + lAC' )/ 2.
2. Проектирование по двум положениям выходного звена .
а)четырехшарнирный механизм
________________________________ Определить: l i - ?
Решение проводится по схеме, которая изображена на рис. 10.13. Положение точки A определяется пересечением луча A С'' , проведенного Рис. 10.13 в точке С'' под углом J = [J ] к вектору скорости VC'' :
с окружностью радиуса l0 (точка Al0 ); с продолжением оси х . Затем, как описано выше, по размерам lAC'и lAC'' определяются длины звеньев 1 и 2.
кривошипно-ползунный механизм дезаксиальный
________________________________ Определить: l i - ?
Решение проводится по схеме, которая изображена на рис. 10.14. Положение точки Ae определяется пересечением луча AС' , проведенного в точке С' под Рис. 10.14 углом J = [J ] к вектору скорости VC' с продолжением оси х . Затем, как описано выше, по размерам lAC' и lAC'' определяются длины звеньев 1 и 2.
центральный кривошипно-ползунный механизм ( е = 0 )
l 2 = l2 / l1 , e = 0
Определить: li - ?
Спроецируем векторный контур lAB + lBC = lAC на оси координат:
l1 * cos j 1 + l2 * cos j 2 + hC = l1 + l2 ,
l1 * sin j 1 + l2 * sin j 2 = 0 ,
l1 / l2 * sin [ J ] или l2 / l1 = l 2 ;
откуда
l1 = hC / { 1-cos j 1 + [ 1 - cos ( arcsin (l 2 ? sin j 1)]/ l 2 },
l2 = l1 / l 2 .
3. Проектирование кривошипно-ползунного механизма по средней скорости ползуна .
Дано: HC , kV = 1 , e = 0 , [ J ] , n1ср
________________________________
Определить: li - ?
Средняя скорость ползуна
VCср = 2 * HC / T ,
где T = 1/ n1ср - период или время одного оборота кривошипа в с,
HC = 2* l1 - ход ползуна.
Размеры звеньев механизма
l1 = VCср / ( 4* n1ср ) , l2 = l1 / l 2 .
Проектирование кулисного механизма по углу давления .
Дано: HD , b , [ J ]
_______________________
Определить: li - ?
Если расположить центр пары А на прямой соединяющей точки С' и С'' , то углы давления
J' = J' = b / 2,
тогда
l C' C'' »HD = 2 * l1 *sin (b / 2)
и l1 = HD / [2* sin (b / 2)].
Минимальная длина гидроцилиндра
lCDmin = k * HD ,
где k = 1.05 - 1.3 - коэффициент учитывающий особенности конструкции гидроцилиндра ( уплотнение, расположение опоры А и др. ).
Размер l4 можно определить из D BC? A
и
_____________________________
Определить: li , h - ?
Угловой ход кулисы
______________________________
Из D АВС длина звена 1
l1 = l0 *sin(b 3/2) = l0*sin(q /2).
Из D СD? q длина звена 3
l3 = HE / [2*sin(b 3/2)] = HE / [2*sin(q /2)] .
Длина звена 4 определяется по допустимому углу давления
sin J = (l3 - h)/l4 * sin [ J ].
Принимаем dq = qf , где dq = l3 * [ 1 - cos (q /2)], тогда
h = l3 * {1 - [ 1- cos (q /2)]/2},
l4 * ( l3 - h )/ sin [ J ] или l4 * ( l3*[ 1- cos (q /2)])/(2* sin [ J ]).
Оптимальный синтез рычажных механизмов.
Согласно энциклопедическому словарю, задача оптимального проектирования - это экономико-математическая задача, содержащая критерий оптимальности и ограничения и направленная на поиск лучшего в определенных условиях (т.е оптимального) значения показателя. Оптимизация - отыскание такого решения рассматриваемой задачи, которое дает экстремальное (минимальное или максимальное) значение некоторой функции, называемой целевой [ Ю.А.Казик Математический словарь. Таллин. “Валгус” 1985 ].
При оптимальном метрическом синтезе механизма необходимо определить такое сочетание его размеров (внутренние параметры), которое наилучшим образом удовлетворяет требуемым эксплуатационным и качественным показателям (критерии оптимизации и ограничивающие условия). При метрическом синтезе в качестве качественных показателей обычно используются: габариты механизма, точность обеспечения заданных положений или закона движения (функции положения или передаточной функции), условия передачи сил в КП (углы давления в КП) и другие показатели.
Механизм при оптимальном проектировании характеризуется двумя n-мерными векторами: параметров и качественных показателей. На значения как парметров, так и качественных показателей могут быть наложены некоторые ограничения в виде равенств или неравенств. Ограничения могут быть:
параметрическими (например, ограничения на длины звеньев механизмов); дискретизирующими (например, выбор размеров из стандартного ряда); функциональными (например, условия проворачиваемости звеньев механизма, условия заклинивания КП). Ограничения формируют область допустимых значений параметров, в пределах которой осуществляется поиск оптимального решения. В пределах этой области могут существовать локальные и глобальный оптимум целевой функции. Целевая функция может быть одномерной или многомерной. При многомерной оптимизации необходимо формирование сложной целевой функции, учитывающей вес каждого из качественных показателей, например, аддитивной
Ф ( G , d , J , ... ) = k1*G + k2*d + k3*J + ...
или мультипликативной функции
Ф ( G , d , J , ... ) = G k1 *d k2 * J k3 ? ...
где Ф ( G , d , J , ... ) - целевая функция, G - габариты механизма, d - точность механизма, J - углы давления в КП механизма, ki - весовые коэффициенты при качественных показателях.
На рис. 10.17 представлена целевая функция при однопараметрической оптимизации ( р - параметр оптимизируемой системы ). Ограничения по параметру рmin и pmax определяют область допустимых решений (ОДР), в пределах которой проводится поиск оптимального решения. В нашем примере в этой области целевая функция имеет два минимума: локальный при рл.опт и глобальный при ргл.опт .
Методы решения задач оптимизации весьма разнообразны и являются предметом изучения в таких учебных дисциплинах как вычислительная математика, математическое программирование, САПР .
Синтез механизма по заданной функции положения.
Дано: Структурная схема механизма, функция положения выходного звена j 3 = П (j 1) на рабочем перемещении D j 3 при начальном положении j 30 .
Определить: Размеры звеньев механизма, обеспечивающие наилучшее приближение к заданной функции.
Предположим, что синтезируется четырехшарнирный механизм. Тогда необходимо определить размеры всех четырех звеньев механизма и начальное значение обобщенной координаты j 10 , т.е. пять неизвестных. Так как решается задача метрического синтеза, а абсолютные размеры звеньев определяются прочностными характеристиками, рабочими нагрузками и материалами, то целесообразно перейти к относительным размерам звеньев, приняв длину одного из них (например, стойки) равной единице. Общее число неизвестных, таким образом, сократится до четырех. Изобразим расчетную схему синтезируемого механизма и заданную функцию положения (рис. 10.18). Выберем на функции положения случайным образом (либо по какой-нибудь стратегии) четыре точки с координатами выходного звена j 31 ,j 32 ,j 33, j 34 . Для каждого из положений можно записать векторное уравнение или два уравнения в проекциях на оси координат (ось абсцисс совпадает с вектором l0 ):
l1 + l2 = l3 + l0 , l1 * sin j 1 + l2 * sin j 2 = l3 * sin j 3 ,
l1 * cos j 1 + l2 * cos j 2 = l3 * cos j 3 + l0 .
Из этой системы определим размеры звеньев механизма и начальное значение координаты j 10. Функция положения синтезированного таким образом механизма будет совпадать с заданной функцией в выбранных точках – узлах интерполяции. Наибольшие отклонения заданной и полученной функций будут находится между узлами интерполяции (рис.10.18). Изменяя положение узлов интерполяции в пределах рабочего перемещения выходного звена можно уменьшать отклонения полученной функции положения от заданной.При использовании метода наименьших квадратов число точек должно быть больше чем число неизвестных (хотя бы на единицу). Полученная функция положения при этом проходит не через узлы интерполяции, а так чтобы отклонения сумма квадратов отклонений в заданных точках была минимальна.
Понятие о геометрических и кинематических характеристиках механизмов
|
Краткое содержание: Понятие о геометрических и кинематических характеристиках механизмов (функция положения и ее производные по времени и по обобщенной координате). Методы определения геометро-кинематических характеристик механизма. Цикл и цикловые графики. Связь между кинематическими и геометрическими параметрами. Кинематическое исследование типовых механизмов: рычажных, зубчатых, кулачковых, манипуляторов.
Понятие о геометрических и кинематических характеристиках механизмов.
Функцией положения механизма называется зависимость углового или линейного перемещения точки или звена механизма от времени или обобщенной координаты.
Геометрические и кинематические характеристики механизма
 |
| Рис. 3.1 |
Кинематическими передаточными функциями механизма называются производные от функции положения по обобщенной координате. Первая производная называется первой передаточной функцией или аналогом скорости (обозначается Vq,wq), вторая - второй передаточной функцией или аналогом ускорения (обозначается aq, eq).
Кинематическими характеристиками механизма называются производные от функции положения по времени. Первая производная называется скоростью (обозначается V, w), вторая - ускорением (обозначается a, e).
Механизм с одной подвижностью имеет одно заданное входное движение и бесчисленное множество выходных ( движение любого звена или точки механизма ). Передаточные функции тех движений, которые в данном случае используются как выходные, называются главными, остальные - вспомогательными.
Рассмотрим схему механической системы образованной последовательно-параллельным соединением типовых механизмов. Схема включает входное звено, зубчатую передачу , кулачковый и рычажный механизмы и имеет два выходных звена.
Схема механической системы
 |
| Рис. 3.2 |
 |
| Рис. 3.3 |
Функции положения в механизмах
 |
| Рис. 3.4 |
Методы геометро-кинематического исследования механизмов
планов положений, скоростей и ускорений, проекций векторного контура, кинематических диаграмм, центроид, преобразования координат, экспериментальный, другие.Связь кинематических и передаточных функций
Линейные скорости и ускорения
VL= dSL / dt = (dSL / df1) * (df1 / dt) = VqL * w1;
a L = d(Vql * w1) / dt = (dVqL / df1) * (df1 / dt) * w1 + Vql * e1 = aqL * w12 + VqL * e1;
Угловые скорости и ускорения
wi = dfi / dt = (dfi / df1) * (df1 / dt) = wqi * w1;
ei = d(wqi * w1) / dt = (dwi / df1) * (df1 / dt) * w1 + wqi * e1 = eqi * w12 + wqi * ei.
Так как данные формулы получены как производные от скалярных величин, то при операциях с векторными величинами они применимы только для проекций этих величин на оси координат.
1. Метод проекций векторного контура. (Рычажные механизмы).
Рассмотрим простейший кулисный механизм.
 |
| Рис. 3.5 |
Заменим кинематическую схему механизма эквивалентным векторным контуром
Тогда уравнение замкнутости векторного контура запишется:
 |
1. 1. Задача о положениях звеньев механизма
 |
| Рис. 3.6 |
Проецируем векторный контур на оси координат и получаем координаты точки В механизма:
xB = lAB * cos (f1) = lAD * cos (p) + lDB * cos (f3);
yB = lAB * sin (f1) = lAD * sin (p) + lDB * sin (f3);
из решения этой системы уравнений определяем неизвестные величины f3 и lDB, которые определяют положение звеньев и точек механизма
tg (f3 ) = sin (f3) / cos (f3) = lAB * sin (f1) / (lAB * cos (f1) - lAD * cos (p));
lDB = (lAB * sin (f1) / sin (f3);
1. 2. Задача о первых кинематических передаточных функциях механизма
Продифференцируем уравнения проекций векторного контура по обобщенной координате и получим
VqBx = -lAB * sin (f1) = VqDB * cos (f3) - lDB * wq3 * sin (f3);
VqBy = lAB * cos (f1) = VqDB * sin (f3) + lDB * wq3 * cos (f3).
Из этой системы уравнений определяем первые передаточные функции VqB и wq3.
1. 3. Задача о вторых передаточных функциях механизма.
Вторично продифференцируем уравнения проекций векторного контура по обобщенной координате и получим
aqBx = -lAB * cos (f1) = aqDB * cos (f3) - 2 * VqDB * w3 * sin (f3) - lDB * eq3 * sin (f3) - lDB*
* w32 * cos (f3);
aqBy = -lAB * sin (f1) = aqDB * sin (f3) + 2 * VqDB * w3 * cos (f3) + lDB * eq3 * cos (f3) - lDB *
* w32 * sin (f3);
Из этой системы уравнений определяем вторые передаточные функции aqB и eq3.
 |
Цикловые кинематические (геометрические) диаграммы для кулисного механизма. Циклом называется период времени или изменения обобщенной координаты по истечении которого все параметры системы принимают первоначальные значения. Поэтому значения величин в начале и в конце цикла одинаковы. |
||
| Рис. 3.7 |
Метод центроид (Зубчатые передачи).
Центроидой (полоидой) называется геометрическое место центров (полюсов) относительного вращения в системах координат связанных со звеньями механизма. В зубчатом механизме при передаче движения центроиды колес перекатываются друг по другу без скольжения.
Схема зубчатого механизма
 |
| Рис. 3.8 |
Повернем ведущее колесо на малый угол df1, тогда ведомое колеса повернется на угол df1.Так как центроиды или начальные окружности колес перекатываются друг по другу без скольжения , то дуга dSw1будет равна дуге dSw2. Тогда можно записать следующее равенство:
dSw1 = dSw2 = dSw,
где: dSw1 = rw1 * df1, dSw2 = rw2 df2.
Откуда: u21 = df2 / df1 = rw1 / rw2 = const.
Функция положения для выходного звена зубчатой передачи
 |
Вторая передаточная функция для выходного звена зубчатой передачи
eq2 = dU21 / df1 = 0.
Механизм зубчатой передачи не является цикловым механизмом, так как угловое перемещение выходного звена увеличивается при увеличении углового перемещения входного. Поэтому кинематические диаграммы построим только для одного оборота входного звена.
 |
Диаграммы функции положения и передаточных функций для зубчатой передачи. 3. Метод цикловых кинематических диаграмм (кулачковые механизмы). Кулачковым называется трехзвенный механизм состоящий из двух подвижных звеньев - кулачка и толкателя, соединенных между собой высшей кинематической парой. Часто в состав механизма входит третье подвижное звено - ролик, введенное в состав механизма с целью замены в высшей паре трения скольжения трением качения. При этом механизм имеет две подвижности одну основную и одну местную (подвижность ролика). Основные параметры кулачкового механизма: fраб - фазовый рабочий угол кулачкового механизма; fраб = dраб = fc + fдв + fу; fс - угол сближения; fдв - фазовый угол дальнего выстоя; fу - фазовый угол удаления; dраб - профильный рабочий угол; fбв - угол ближнего выстоя; hBm - максимальное перемещение точки В толкателя; r0 - радиус начальной шайбы кулачка; rр - радиус ролика. |
||
| Рис. 3.9 |
 |
| Рис. 3.10 |
 |
| Рис. 3.11 |
При кинематическом анализе кулачкового механизма задан конструктивный профиль кулачка и радиус ролика rp. Методом обращенного движения (перекатывая ролик по неподвижному конструктивному профилю кулачка) находим центровой профиль кулачка (траекторию центра ролика толкателя в обращенном движении). Наносим на профиль фазовые углы и определяем в зоне ближнего выстоя начальный радиус центрового профиля кулачка r0. В зоне рабочего угла проводим ряд траекторий центра ролика толкателя (точки В) и по ним измеряем от точки лежащей на окружности r0 до точки лежащей на центровом профиле текущее перемещение толкателя SBi. По этим перемещениям строим диаграмму SB = f(f1). Дифференцируя эту диаграмму по времени или обобщенной координате получаем кинематические или геометрические характеристики механизма. При графическом дифференцировании масштабы диаграмм зависят от масштабов исходной диаграммы и выбранных отрезков дифференцирования:
mS = yhb / hB мм/м; mf = b / fр мм/рад; mt = b/tрмм/с;
mVq = k1 * mS / mf мм/м; maq = k2 * mVq / mf мм/м;
mV = k1 * mS / mt мм/м*с-1; ma = k2 * mV / mtмм/м*c-2;
где b - база диаграммы по оси абсцисс в мм, yhB - ордината максимального перемещения толкателя в мм, hB - максимальное перемещение толкателя в м, tр - время поворота кулачка на фазовый угол fрв с, k1 и k2 - отрезки дифференцирования в мм.
4. Метод преобразования координат (Манипуляторы)
При использовании метода преобразования координат задача о положении выходного звена решается путем перехода из системы в которой это положение известно в систему в которой его требуется определить. Переход от системы к системе осуществляется перемножением матриц перехода в соответствующей последовательности.
4. 1. Формирование матрицы перехода для плоских механизмов.
 |
| Рис. 3.12 |
 |
Тогда векторы столбцы координат точки М и матрица перехода из системы j в систему i
 |
Векторное уравнение перехода из системы j в систему i
 |
Пример применения метода преобразования координат для плоского трехподвижного манипулятора:
 |
| Рис. 3.13 |
5. Экспериментальный метод кинематического исследования.
При экспериментальном исследовании кинематики механизмов кинематические характеристики звеньев и точек механизма определяются и регистрируются с помощью чувствительных элементов - датчиков, которые используя различные физические эффекты преобразуют кинематические параметры в пропорциональные электрические сигналы. Эти сигналы регистрируются измерительными самопишущими приборами (самописцами, осциллографами и др.). В последнее время для регистрации и обработки экспериментальных данных все более широко используются специальные или универсальные компьютеры. Для примера рассмотрим экспериментальную установку для исследования кинематических характеристик синусного механизма:
 |
| Рис. 3.14 |
для измерения перемещения выходного звена используется потенциометрический датчик перемещения, в котором пропорционально положению движка потенциометра изменяется его сопротивление;
для измерения скорости выходного звена используется идукционный датчик скорости, в котором напряжение на концах катушки движущейся в поле постоянного магнита пропорционально скорости катушки;
для измерения ускорения выходного звена используется тензометрическиий акселерометр. Он состоит из пластинчатой пружины один конец которой закреплен на выходном звене механизма, а на втором закреплена масса. На пластину наклеены проволочные тензопреобразователи. При движении выходного звена с ускорением инерционность массы вызывает изгиб пластины , деформацию тензопреобразователей и изменение их сопротивления пропорциональное ускорению выходного звена.
Передаточные функции механизмов с несколькими подвижностями (W>1).
Рассмотрим простой двухподвижный манипулятор
 |
| Рис. 3.15 |
f2 = P(f10,f21),
и ее производная определится как производная функции двух переменных:
df2 = [dP(f10,f21) / df10] df10 + [dP(f10,f21) / df21] df21 = wq10 * df10 + wq21 * df21,
где wq10 и wq21 - частные производные по обобщенным координатам.
Постановка задачи синтеза
|
Краткое содержание:
[Постановка задачи синтеза]
[Условия подбора чисел зубьев. Вывод расчетных формул для условий соосности, соседства и сборки]
[Подбор чисел зубьев по методу сомножителей]
[Примеры решения задач по подбору чисел зубьев]
[Оптимальный синтез планетарных механизмов при автоматизированном проектировании]
Проектирование многопоточных планетарных механизмов:
Постановка задачи синтеза:
При проектировании многопоточных планетарных механизмов необходимо, кроме требований технического задания, выполнять ряд условий связанных с особенностями планетарных и многопоточных механизмов. Задача проектирования и в этом случае может быть разделена на структурный и метрический синтез механизма. При структурном синтезе определяется структурная схема механизма, при метрическом – определяются числа зубьев колес, так как радиусы зубчатых прямо пропорциональны числам зубьев ri = m Ч zi / 2.
Для типовых механизмов первая задача сводится к выбору схемы из набора типовых схем. При этом руководствуются рекомендуемым для схемы диапазоном передаточных отношений и примерными оценками ее КПД. Для рассматриваемых схем эти данные приведены в таблице 15.1. После выбора схемы механизма необходимо определить сочетание чисел зубьев его колес, которые обеспечат выполнение условий технического задания – для редуктора это передаточное отношение и величина момента сопротивления на выходном валу. Передаточное отношение задает условия выбора относительных размеров зубчатых колес – чисел зубьев колес, крутящий момент задает условия выбора абсолютных размеров – модулей зубчатых зацеплений. Так как для определения модуля необходимо выбрать материал зубчатой пары и вид его термообработки, то на первых этапах проектирования принимают модуль зубчатых колес равным единице, то есть решают задачу кинематического синтеза механизма в относительных величинах.
При кинематическом синтезе (подборе чисел зубьев колес) задача формулируется так: для выбранной схемы планетарного механизма при заданном числе силовых потоков (или числе сателлитов k) и заданном передаточном отношении u необходимо подобрать числа зубьев колес zi, которые обеспечат выполнение ряда условий.
Условия подбора чисел зубьев.
Вывод расчетных формул для условий соосности, соседства и сборки: Условия, которые необходимо выполнить при подборе чисел зубьев колес типового планетарного механизма:
заданное передаточное отношение с требуемой точностью
соосность входного и выходного валов механизма свободное размещение (соседство) сателлитов сборку механизма при выбранных числах зубьев колес отсутствие подреза зубьев с внешним зацеплением отсутствие заклинивания во внутреннем зацеплении минимальные относительные габариты механизма. Рассмотрим эти условия подробнее на примере двухрядного планетарного механизма с одним внешним и одним внутренним зацеплением.
Рис. 16.1

Обеспечение заданного передаточного отношения с требуемой точностью:
Принимаем требуемую точность ± 5%, тогда для рассматриваемой схемы механизма
u1h = [ 1+ (z2 Ч z4)/(z1 Ч z3) ] Ч ( 0.95 … 1.05 ).
Обеспечение соосности входного и выходного валов:
Для этого необходимо чтобы межосевое расстояние в передаче внешнего зацепления (первый ряд) равнялось межосевому расстоянию в передаче внутреннего зацепления (второй ряд), то есть
awI = awII ; awI= rw1 + rw2 = r1 + r2 ; awII = rw4 - rw3 = r4 - r3. Обычно в планетарных механизмах применяются зубчатые колеса без смещения, для которых xi = 0 и rwi = ri = zi Ч m / 2.Тогда
r1 + r2= r4 - r3Ю mI ( z1 + z2) = mIIЧ (z4 - z3). Принимаем, что mI = mII = m, и получаем условие соосности для данной схемы механизма
| z1 + z2 = z4 - z3 |
Обеспечение условия соседства сателлитов (при числе сателлитов k > 1):
Сателлиты размещаются на окружности радиуса aw.
Вершины зубьев сателлитов не будут мешать движению друг друга, если выполняется условие
max ( da2,3 ) < lB2B3. Для зубчатых колес без смещения ( ha*= 1, x2,3 = 0, 2Dy = 0 ) максимальный из диаметров сателлитов равен
max ( da2,3 ) = max [( z2,3 + 2 Ч ha* +2 Ч x2,3 - 2Dy) Ч m ] = max[( z2,3 + 2) Ч m ]. Расстояние между осями сателлитов
lB2B3 = 2 Ч aw Ч sin ( jh / 2 ) = 2 Ч (r1 + r2) Ч sin ( p / k ). = (z1 + z2) Ч m Ч sin ( p / k ). Подставим полученные выражения в неравенство и получим условие соседства
max [( z2,3 + 2) Ч m ] < (z1 + z2) Ч m Ч sin (p / k).
| sin ( p /k ) > max [( z2,3 + 2)/ (z1 + z2) ] |
Обеспечить возможность сборки механизма с подобранными числами зубьев колес при заданном числе сателлитов k > 1:
Для вывода формулы условия сборки воспользуемся следующим методом: Допустим, что все сателлиты устанавливаются на оси водила в одном и том же положении – точке В1. После установки первого сателлита, зубья колес z1и z4определенным образом установились относительно зубьев венцов сателлита. Тогда установить второй сателлит в этом же положении будет можно, если после поворота водила на угол jh колесо z1 повернется на целое число угловых шагов В. При этом зубья колес z1 и z4установятся относительно зубьев венцов сателлита так же, как и при установке первого сателлита. Угол поворота водила Юjh= 2 Ч p / k
Угловой шаг первого колеса Юt1 = 2 Ч p / z1
Угол на который повернется первое колесо при повороте водила на угол jh
j1 = jhЧ u1h Юj1 = 2 Ч p Ч u1h / k Число угловых шагов t1в угле j1 Ю B = j1 / t1, где B - произвольное целое число. Подставляем все эти выражения в формулу для B и после преобразований получаем
2 Ч pЧ u1h Ч z1 / (k Ч 2 Чp) = B Ю
| u1h Ч z1 / k = B. |
jh= 2 Ч p / k + 2 Ч pЧ р = 2 Чp / k ( 1 + k Ч р). С учетом этого, формула для условия сборки примет следующий вид:
| u1h Ч z1 / k ( 1 + k Ч р) = B. |
Обеспечить отсутствие подрезания колес с внешними зубьями зубьев:
Это условие обеспечивается, если для всех колес с внешними зубьями выполняется неравенство zi > zmin.
Обеспечить отсутствие заклинивания во внутреннем зацеплении:
Это условие для передачи внутреннего зацепления, состоящей из колес без смещения, можно обеспечить при выполнении следующих неравенств
| z с внеш. зуб. > 20, z с внутр. зуб. > 85, zd = z с внутр. зуб - z с внеш. зуб. > 8. |
Обеспечить минимальные габариты механизма.
Для рассматриваемой схемы условие обеспечения минимального габаритного размера R можно записать так
R = min [ max ( z1 + 2 Ч z2 ), (kK Ч z4) ], где kK - коэффициент, учитывающий особенности конструкции зубчатого колеса с внутренними зубьями. Подбор чисел зубьев по методу сомножителей:
Рассмотрим один из методов, используемых при подборе чисел зубьев планетарного редуктора, - метод сомножителей. Метод позволяет объединить в расчетные формулы некоторые из условий подбора (условия 1, 2, 5 и 6). Выполнение остальных условий для выбранных чисел зубьев проверяется. Из первого условия выразим внутреннее передаточное отношение механизма. Внутренним называют передаточное отношение механизма при остановленном водиле, то есть механизма с неподвижными осями или рядного механизма. u14 h = (z2 Ч z4)/(z1 Ч z3) = [ u1h / ( 0.95 … 1.05 ) – 1] = (B Ч D)/(A Ч C). Разложим внутреннее передаточное отношение u14 hна сомножители - некоторые целые числа A, B, C иD.При этом сомножитель Aсоответствует числу зубьев z1 , B - z2 , C - z3 и D - z4.Сомножители могут быть произвольными целыми числами, комбинация (B Ч D) / (A Ч C) которых равна u14 h.
Для рассматриваемой схемы желательно придерживаться следующих диапазонов изменения отношений между сомножителями B / A = z2 / z1 = 1 … 6 -внешнее зацепление, D / C = z4 / z3 = 1.1 … 8 – внутреннее зацепление. Включим в рассмотрение условие соосности:
z1 + z2 = z4 - z3 и выразим его через сомножители
a Ч ( A + B) = b Ч ( D – C ). Если принять, что коэффициенты a и b равны
a = ( D – C ), b = (A + B), то выражение превращается в тождество.
Из этого тождества можно записать:
z1= ( D – C ) Ч A Ч q, z3= ( A + B ) Ч C Ч q,
z2= ( D – C ) Ч B Ч q, z4= ( A + B ) Ч D Ч q. где q - произвольный множитель, выбором которого обеспечиваем выполнение условий 5 и 6. Зубья колес планетарного механизма, рассчитанные по этим формулам, удовлетворяют условиям 1, 2, 5 и 6. Проверяем эти зубья по условиям 3 (соседства) и 4 (сборки) и если они выполняются, считаем этот вариант одним из возможных решений.
Если после перебора рассматриваемых сочетаний сомножителей получим несколько возможных решений, то проводим их сравнение по условию 7. Решением задачи будет сочетание чисел зубьев, обеспечивающее габаритный минимальный размер R. Примеры подбора чисел зубьев для типовых планетарных механизмов: 1. Двухрядный планетарный редуктор с одним внешним и с одним внутренним зацеплением. Дано: Схема планетарного механизма, u1h = 13, k = 3.
Определить: zi - ? Внутреннее передаточное отношение механизма:
u14 h = (z2 Ч z4) / (z1 Ч z3) = [ u1h / ( 0.95 … 1.05 ) – 1] = 12 = (B Ч D)/(A Ч C) = 3 Ч 4 / (1 Ч 1) = 2 Ч 6 / (1 Ч 1)= 4 Ч 3 / (1 Ч 1) = ... Для первого сочетания сомножителей:
z1= ( D – C ) Ч A Ч q = ( 4 – 1 ) Ч 1 Ч q = 3 Ч q ; z1= 18 > 17;
z2= ( D – C ) Ч B Ч q = ( 4 – 1 ) Ч 3 Ч q = 9 Ч q ; q = 6; z2= 54 > 17;
z3= ( A + B ) Ч C Ч q = ( 3 + 1 ) Ч 1 Ч q = 4 Ч q; z3= 24 > 20;
z4= ( A + B ) Ч D Ч q = ( 3 + 1 ) Ч 4 Ч q = 16 Ч q; z4= 96 > 85; Проверка условия соседства:
sin ( p / k ) > max [( z2,3 + 2)/ (z1 + z2) ]
sin ( p / 3 ) > (54 + 2)/(18+54)
0.866 > 0.77 - условие выполняется. Проверка условия сборки:
( u1h Ч z1 / k ) Ч ( 1 + k Ч p) = B;
(13 Ч 18/3) Ч ( 1 + 3 р) = В - целое при любом p. Условие сборки тоже выполняется. То есть, получен первый вариант решения!
Габаритный размер R = (18 + 2 Ч 54) = 126. Для второго сочетания сомножителей:
z1= ( D – C ) Ч A Ч q = ( 6 – 1 ) Ч 1 Ч q = 5 Ч q ; z1= 45 > 17;
z2= ( D – C ) Ч B Ч q = ( 6 – 1 ) Ч 2 Ч q = 10 Ч q ; q = 9; z2= 90 > 17;
z3= ( A + B ) Ч C Ч q = ( 2 + 1 ) Ч 1 Ч q = 3 Ч q; z3= 27 > 20;
z4= ( A + B ) Ч D Ч q = ( 2 + 1 ) Ч 6 Ч q = 18 Ч q; z4= 162 > 85; Проверка условия соседства:
sin ( p / k ) > max [( z2,3 + 2)/ (z1 + z2) ]
sin ( p / 3 ) > (90 + 2)/(45+90)
0.866 > 0.681 - условие выполняется. Проверка условия сборки:
( u1h Ч z1 / k ) Ч ( 1 + k Ч р) = B
(12 Ч 45 / 3) Ч ( 1 + 3 р) = В - целое при любом р. Условие сборки тоже выполняется и получен второй вариант решения!
Габаритный размер R = (45 + 2 Ч 90) = 225. Для третьего сочетания сомножителей:
z1= ( D – C ) Ч A Ч q = ( 3 – 1 ) Ч 1 Ч q = 2 Ч q ; z1= 18 > 17;
z2= ( D – C ) Ч B Ч q = ( 3 – 1 ) Ч 4 Ч q = 8 Ч q ; q = 9; z2= 72 > 17;
z3= ( A + B ) Ч C Ч q = ( 1 + 4 ) Ч 1 Ч q = 5 Ч q; z3= 45 > 20;
z4= ( A + B ) Ч D Ч q = ( 1 + 4 ) Ч 3 Ч q = 15 Ч q; z4= 135 > 85; Проверка условия соседства:
sin ( p / k ) > max [( z2,3 + 2)/ (z1 + z2) ]
sin ( p / 3 ) > (70 + 2)/(18+72)
0.866 > 0.8 - условие выполняется. Проверка условия сборки:
( u1h Ч z1 / k ) Ч ( 1 + k Ч р) = B
(13 Ч 18/3) Ч ( 1 + 3 р) = В - целое при любомр. Условие сборки тоже выполняется и получен третий вариант решения.
Габаритный размер R = (18 + 2 Ч 72) = 162. Из рассмотренных трех вариантов габаритный наименьший размер получен в первом. Этот вариант и будет решением нашей задачи. 2. Однорядный механизм с одним внутренним и одним внешним зацеплением.
Рис. 16.2  |
Дано: схема планетарного механизма, u1h = 7; k = 3. Определить: zi - ?. |
z1 = 18 > 17. Тогда из формулы передаточного отношения можно определить число зубьев третьего колеса:
u1h = ( 1 + z3 / z1 ) Ч (0.95 … 1.05)
z3 = [u1h / (0.95…1.05) - 1] Ч z1
z3 = [ 7 / (0.95…1.05) - 1] Ч 18 = 108 Число зубьев второго колеса определим из условия соосности:
z1 + z2 = z3 - z2
z2 = ( z3 - z1 ) / 2 = ( 108 - 18 ) / 2 = 45 Проверка условия соседства:
sin ( p / k ) > max [( z2 + 2)/ (z1 + z2) ]
sin ( p / 3 ) > (45 + 2)/(18+45)
0.866 > 0.73 - условие выполняется. Проверка условия сборки:
( u1h Ч z1 / k ) Ч ( 1 + k Ч р) = B
(7 Ч 18/3) Ч ( 1 + 3 р) = В целое при любом р. В данном случае нет необходимости сравнивать варианты по габаритам, так как мы приняли минимально допустимую величину z1
,то получим редуктор с минимальных размеров. 3. Двухрядный механизм с двумя внешними зацеплениями.
Рис. 16.3  |
Дано: схема планетарного механизма, uh1 = -24; k =3. Определить: zi - ?. |
u1h= 1 / uh1
u14 h = (z2 Ч z4)/(z1 Ч z3) = [ 1 - u1h / ( 0.95 … 1.05 ) ] = 25/24 = (B Ч D)/(A Ч C) = 5 Ч 5 / (4 Ч 6) = 5 Ч 5 / (6 Ч 4)= 25 Ч 1 / (12 Ч 2) = ... Условие соосности для этой схемы:
z1 + z2 = z4 + z3 и выразим его через сомножители:
a Ч ( A + B) = b Ч ( D + C ). Принимаем коэффициенты a и b:
a = ( D + C ), b = (A + B). и получаем для сочетания сомножителей обведенного рамкой:
z1= ( D + C ) Ч A Ч q = ( 1 + 2 ) Ч 12 Ч q = 36 Ч q ; z1= 36 > 17;
z2= ( D + C ) Ч B Ч q = ( 1 + 2 ) Ч 25 Ч q = 75 Ч q ; q = 1; z2= 75 > 17;
z3= ( A + B ) Ч C Ч q = ( 12 + 25 ) Ч 2 Ч q = 74 Ч q; z3= 74 > 17;
z4= ( A + B ) Ч D Ч q = ( 12 + 25 ) Ч 1 Ч q = 37 Ч q; z4= 37 > 17; Проверка условия соседства:
sin ( p / k ) > max [( z2,3 + 2)/ (z1 + z2) ];
sin ( p / 3 ) > (75 + 2)/(36+75)
0.866 > 0.694 - условие выполняется. Проверка условия сборки:
( u1h Ч z1 / k ) ? ( 1 + k Ч р) = B;
[18 / (-24Ч 3)] Ч( 1 + 3 р) = В - целое прир=1. Условие сборки тоже выполняется. То есть, получен первый вариант решения.
Габаритный размер R = (36 + 2 Ч 75) = 186. Аналогичным образом рассматриваются другие сочетания сомножителей и из вариантов, удовлетворяющих первым шести условиям, выбирается тот, который обеспечивает наименьшие габариты. 4. Двухрядный механизм с двумя внутренними зацеплениями.
Рис. 16.4  |
Дано: схема планетарного механизма, u1h = 55; k = 2. Определить: zi - ?. |
u1h= 1 / uh1;
u14 h = (z2 Ч z4)/(z1 Ч z3) = [ 1 - u1h / ( 0.95 … 1.05 ) ] = 54 / 55 = (B Ч D)/(A Ч C) = 6 Ч 9 / (11 Ч 5) = 18 Ч 3 / (55 Ч 1) = ... Условие соосности для этой схемы:
z1 - z2 = z4 - z3 и выразим его через сомножители:
a Ч ( A - B) = b Ч ( D - C ) Принимаем коэффициенты a и b:
a = ( D - C ), b = (A - B) и получаем для сочетания сомножителей обведенного рамкой:
z1= ( D - C ) Ч A Ч q = ( 3 - 1 ) Ч 55 Ч q = 110 Чq ; z1= 110 > 85;
z2= ( D - C ) Ч B Ч q = ( 3 - 1 ) Ч 18 Ч q = 36 Ч q ; q = 1; z2= 36 > 20;
z3= ( A - B ) Ч C Ч q = ( 55 - 18 ) Ч 1 Ч q = 37 Ч q; z3= 37 > 20;
z4= ( A - B ) Ч D Ч q = ( 55 - 18 ) Ч 3 Ч q = 111 Ч q; z4= 111 > 85; Проверка условия соседства:
sin ( p /k ) > max [( z2,3 + 2)/ (z1 + z2) ]
sin ( p /2 ) > (37 + 2)/(110 - 36)
1.0 > 0.527 - условие выполняется. Проверка условия сборки:
( u1h Ч z1 / k ) Ч ( 1 + k Ч р) = B;
[110 / (55 Ч 2)] Ч ( 1 + 3 р) = В - целое при любом р. Условие сборки тоже выполняется. То есть, получен первый вариант решения.
Габаритный размер R = (1.2 Ч 111 ) = 133.2, при kK = 1.2. Аналогичным образом рассматриваются другие сочетания сомножителей и из вариантов, удовлетворяющих первым шести условиям, выбирается тот, который обеспечивает наименьшие габариты. Оптимальный синтез планетарных механизмов при автоматизированном проектировании: При автоматизированном проектировании с помощью компьютера можно за относительно небольшой промежуток времени получить большое количество возможных решений задачи. Сопоставляя эти решения между собой находят то, которое удовлетворяет всем требованиям наилучшим образом. При этом перебор вариантов осуществляется в пределах заданных ограничений на параметры (в данном случае на числа зубьев колес) по какой-либо стратегии или чаще случайным образом. Программы оптимального синтеза могут использовать рассмотренные выше методы (например, метод сомножителей), а могут просто перебирать допустимые сочетания параметров и проверять их на соответствие заданным условиям. Использование компьютерных программ для синтеза планетарных механизмов позволяет существенно сократить время проектирования и существенно улучшить качественные показатели спроектированных механизмов. Планетарные механизмы с двумя подвижностями (дифференциалы): На практике в качестве механизмов с двумя подвижностями наиболее часто применяются планетарные зубчатые механизмы или как их еще называют планетарные дифференциалы.
Это название справедливо для механизмов, в которых входной энергетический поток разделяется на два выходных потока. Если входные энергетические потоки суммируются на выходе в один выходной поток, то такие механизмы следует называть суммирующими или интегральными. Все рассмотренные типовые схемы механизмов можно выполнить с двумя подвижностями. Рассмотрим в качестве примера двухрядный механизм с одним внешним и одним внутренним зацеплением (рис.16.5). Рис. 16.5

По формуле Виллиса отношение угловых скоростей звеньев
для внешнего зацепления колес z2 и z1
(w1 - wh) / (w2 - wh) = - z2 / z1 для внутреннего зацепления колес z4 и z3
(w2 - wh) / (w3 - wh) = z4 / z3 . Перемножим, правые и левые части этих уравнений, и получим соотношение между угловыми скоростями механизма с двумя подвижностями
[(w1 - wh) / (w2 - wh)] Ч [(w2-wh)/ (w3-wh)] = - z2 Ч z4 / ( z1 Ч z3)
(w1 - wh) / (w3 - wh) = - z2 Ч z4 / ( z1 Ч z3) = u13(h)
u13 (h) Ч w3 - u13 (h) Ч wh = w1 - wh
| w1 - ( 1 + u13 (h)) Ч wh - u13 (h) Ч w3 = 0 |

Прямая задача динамики машин
|
Прямая задача динамики машин.
Прямая задача динамики машины, как отмечалось и ранее, является задачей анализа, задачей по определению закона движения механической системы под действием заданных внешних сил. При решении этой задачи параметры машинного агрегата и действующие на него внешние силы известны, необходимо определить закон движения: скорости и ускорения в функции времени или обобщенной координаты. Иначе эту задачу можно сформулировать так: заданы управляющие силы и силы внешнего сопротивления, определить обеспечиваемый ими закон движения машины. Обратная задача - это задача синтеза управления, когда задан требуемый закон движения машины и внешние силы сопротивления, а определяются управляющие силы. При решении задач динамики используются либо уравнения силового равновесия системы - метод кинетостатики, либо уравнения энергетического равновесия - закон сохранения энергии. Для идеальной механической системы, в которой не потерь энергии и звенья абсолютно жесткие, этот закон можно применять в виде теоремы о изменении кинетической энергии. Согласно этой теореме работа всех внешних сил действующих на систему расходуется только на изменение ее кинетической энергии. При этом потенциальные силы - силы веса рассматриваются как внешние
Рассмотрим сложную механическую систему (рис.6.1), состоящую из n подвижных звеньев из которых r - звеньев совершают вращательное движение, j - плоское, k - поступательное.
Основная подвижность системы равна W=1. На систему действуют: f - внешних сил и m - внешних моментов. Движение этой системы определяется изменением одной независимой обобщенной координаты. Такую систему при решении задач динамики можно заменить более простой динамической моделью. Положение звена этой модели определяется обобщенной координатой, а динамические параметры заменяются: инерционные - суммарным приведенным моментом инерции Iпрa , силовые - суммарным приведенным моментом Мпрa
. Эти параметры динамической модели рассчитываются по критериям подобия модели и объекта, которые определяются соответственно из равенства правых и левых частей уравнений изменения кинетической энергии для модели и объекта, т.е.
Кинетическая энергия: для механической системы
четырехтактный ДВС
4. Определение суммарного приведенного момента инерции Iпрa . Для определения суммарного приведенного момента инерции необходимо просуммировать приведенные моменты инерции от всех масс и моментов инерции подвижных звеньев рассматриваемой системы. Приведенный момент инерции от массы равен произведению массы на квадрат передаточной функции ее центра, от момента инерции - произведению момента инерции звена на квадрат передаточного отношения от этого звена к звену приведения. Инерционность рассматриваемой системы определяется массами звеньев 2 и 3 и моментами инерции ротора двигателя, редуктора, коленчатого вала, маховика и звена 2. В суммарный приведенный момент инерции входят как составляющие не зависящие от положения механизма, так и составляющие, зависящие от обобщенной координаты. Первые имеют постоянный момент инерции и относятся к первой группе звеньев, момент инерции других - переменный, они образуют вторую группу. Приведенный момент для рассматриваемой системы определяется по формуле:
Промышленные роботы и манипуляторы
|
Краткое содержание: Промышленные роботы и манипуляторы. Назначение и области применения. Классификация промышленных роботов. Принципиальное устройство промышленного робота. Основные понятия и определения.Структура манипуляторов. Геометро-кинематические характеристики.
Промышленные роботы и манипуляторы.
Промышленный робот – автоматическая машина, состоящая из манипулятора и устройства программного управления его движением, предназначенная для замены человека при выполнении основных и вспомогательных операций в производственных процессах.
Манипулятор – совокупность пространственного рычажного механизма и системы приводов, осуществляющая под управлением программируемого автоматического устройства или человека-оператора действия (манипуляции), аналогичные действиям руки человека.
Назначение и область применения.
Промышленные роботы предназначены для замены человека при выполнении основных и вспомогательных технологических операций в процессе промышленного производства. При этом решается важная социальная задача - освобождения человека от работ, связанных с опасностями для здоровья или с тяжелым физическим трудом, а также от простых монотонных операций, не требующих высокой квалификации. Гибкие автоматизированные производства, создаваемые на базе промышленных роботов, позволяют решать задачи автоматизации на предприятиях с широкой номенклатурой продукции при мелкосерийном и штучном производстве. Копирующие манипуляторы, управляемые человеком-оператором, необходимы при выполнении различных работ с радиоактивными материалами. Кроме того, эти устройства незаменимы при выполнении работ в космосе, под водой, в химически активных средах. Таким образом, промышленные роботы и копирующие манипуляторы являются важными составными частями современного промышленного производства.
Классификация промышленных роботов.
Промышленные роботы классифицируются по следующим признакам:
| по характеру выполняемых технологических операций основные; вспомогательные; универсальные; по виду производства литейные; сварочные; кузнечно-прессовые; для механической обработки; сборочные; окрасочные; транспортно-складские; по системе координат руки манипулятора прямоугольная; цилиндрическая; сферическая; сферическая угловая (ангулярная); другие; по числу подвижностей манипулятора; по грузоподъемности сверхлегкие (до 10 Н); легкие (до 100 Н); средние (до 2000 Н); тяжелые (до 10000 Н); сверхтяжелые (свыше 10000 Н); по типу силового привода электромеханический; пневматический; гидравлический; комбинированный; по подвижности основания мобильные; стационарные; по виду программы с жесткой программой; перепрограммируемые; адаптивные; с элементами искусственного интеллекта; по характеру программирования позиционное; контурное; комбинированное. |
Принципиальное устройство промышленного робота.
Манипулятор промышленного робота по своему функциональному назначению должен обеспечивать движение выходного звена и, закрепленного в нем, объекта манипулирования в пространстве по заданной траектории и с заданной ориентацией. Для полного выполнения этого требования основной рычажный механизм манипулятора должен иметь не менее шести подвижностей, причем движение по каждой из них должно быть управляемым. Промышленный робот с шестью подвижностями является сложной автоматической системой. Эта система сложна как в изготовлении, так и в эксплуатации. Поэтому в реальных конструкциях промышленных роботов часто используются механизмы с числом подвижностей менее шести. Наиболее простые манипуляторы имеют три, реже две, подвижности. Такие манипуляторы значительно дешевле в изготовлении и эксплуатации, но предъявляют специфические требования к организации рабочей среды. Эти требования связаны с заданной ориентацией объектов манипулирования относительно механизма робота. Поэтому оборудование должно располагаться относительно такого робота с требуемой ориентацией.
Рассмотрим для примера структурную и функциональную схемы промышленного робота с трехподвижным манипулятором. Основной механизм руки манипулятора состоит из неподвижного звена 0 и трех подвижных звеньев 1, 2 и 3 (рис.19.1).
 |
| Рис. 19.1 |
Для выполнения каждого из трех относительных движений манипулятор должен быть оснащен приводами, которые состоят двигателей с редуктором и системы датчиков обратной связии. Так как движение объекта осуществляется по заданному закону движения, то в системе должны быть устройства сохраняющие и задающие программу движения, которые назовем программоносителями. При управлении от ЭВМ такими устройствами могут быть дискеты, диски CD, магнитные ленты и др. Преобразование заданной программы движения в сигналы управления двигателями осуществляется системой управления. Эта система включает ЭВМ, с соответствующим программным обеспечением, цифроаналоговые преобразователи и усилители. Система управления, в соответствии с заданной программой, формирует и выдает на исполнительные устройства приводов (двигатели) управляющие воздействия ui. При необходимости она корректирует эти воздействия по сигналам Dxi, которые поступают в нее с датчиков обратной связи. Функциональная схема промышленного робота приведена на рис. 19.2.
 |
| Рис. 19.2 |
Основные понятия и определения. Структура манипуляторов.
Геометро-кинематические характеристики.
Формула строения - математическая запись структурной схемы манипулятора, содержащая информацию о числе его подвижностей, виде кинематических пар и их ориентации относительно осей базовой системы координат (системы, связанной с неподвижным звеном).
Движения, которые обеспечиваются манипулятором делятся на:
глобальные (для роботов с подвижным основанием) - движения стойки манипулятора, которые существенно превышают размеры механизма; региональные (транспортные) - движения, обеспечиваемые первыми тремя звеньями манипулятора или его "рукой", величина которых сопоставима с размерами механизма; локальные (ориентирующие) - движения, обеспечиваемые звеньями манипулятора, которые образуют его "кисть", величина которых значительно меньше размеров механизма. В соответствии с этой классификацией движений, в манипуляторе можно выделить два участка кинематической цепи с различными функциями: механизм руки и механизм кисти.
Под "рукой" понимают ту часть манипулятора, которая обеспечивает перемещение центра схвата – точки М (региональные движения схвата); под "кистью" – те звенья и пары, которые обеспечивают ориентацию схвата (локальные движения схвата).
Рассмотрим структурную схему антропоморфного манипулятора, то есть схему которая в первом приближении соответствует механизму руки человека (рис.19.3).
 |
| Рис. 19.3 |
Кинематические пары манипулятора характеризуются: именем или обозначением КП - заглавная буква латинского алфавита (A,B,C и т.д.); звеньями, которые образуют пару (0/1,1/2 и т.п.); относительным движением звеньев в паре ( для одноподвижных пар - вращательное, поступательное и винтовое); подвижностью КП (для низших пар от 1 до 3, для высших пар от 4 до 5); осью ориентации оси КП относительно осей базовой или локальной системы координат.
Рабочее пространство манипулятора - часть пространства, ограниченная поверхностями огибающими к множеству возможных положений его звеньев.
Зона обслуживания манипулятора - часть пространства соответствующая множеству возможных положений центра схвата манипулятора. Зона обслуживания является важной характеристикой манипулятора. Она определяется структурой и системой координат руки манипулятора, а также конструктивными ограничениями наложенными относительные перемещения звеньев в КП.
Подвижность манипулятора W - число независимых обобщенных координат однозначно определяющее положение схвата в пространстве.
 |
 |
 |
 |
Относительная величина ky = y / (4p), называется коэффициентом сервиса. Для манипулятора, изображенного на рис.19.4,
| подвижность манипулятора: W = 6 * 3 - (3 * 2 - 5 * 1) = 18 - 11 = 7; маневренность: M = 7 - 6 = 1; формула строения: W = [q10 + j10 + y10 ] + j21 + [q32 + j32 + y32 ]. |
 |
| Рис. 19.4 |

прямоугольной декартовой с координатами xM, yM, zM; цилиндрической с координатами rsM, j M, zM; сферической с координатами rM, j M, q M. Ориентация объекта в пространстве задается углами a, b и g, которые вектор ориентации

 |
| Рис. 19.5 |
кинематические пары манипуляторов снабжаются приводами, включающими двигатели и тормозные устройства, поэтому в схемах манипуляторов обычно используются одноподвижные кинематические пары: вращательные или поступательные; необходимо обеспечить не только заданную подвижность свата манипулятора, но и такую ориентацию осей кинематических пар, которая обеспечивала необходимую форму зоны обслуживания, а также простоту и удобство программирования его движений; при выборе ориентации кинематических пар необходимо учитывать расположение приводов (на основании или на подвижных звеньях), а также способ уравновешивания сил веса звеньев. При выполнении первого условия кинематические пары с несколькими подвижностями заменяют эквивалентными кинематическими соединениями.
Пример такого соединения для сферической пары дан на рис. 19.6.
Перемещение схвата в пространстве можно обеспечить, если ориентировать оси первых трех кинематических пар по осям одной из осей координат. При этом выбор системы координат определяет тип руки манипулятора и вид его зоны обслуживания. По ГОСТ 25685-83 определены виды систем координат для руки манипулятора, которые приведены в таблице 19.1. Здесь даны примеры структурных схем механизмов соответствующие системам координат. Структурные схемы механизмов кисти, применяемые в манипуляторах, даны в таблице 19.2. Присоединяя к выходному звену руки тот или иной механизм кисти, можно получить большинство известных структурных схем манипуляторов, которые применяются в реальных промышленных роботах.
 |
 |
| Сферическая кинематическая пара |
Эквивалентное кинематическое соединение |
| Системы координат "руки" манипулятора. | Таблица 19.1 |
| Прямоугольная (декартова) | Цилиндрическая |
 |
 |
| Сферическая | Угловая (ангулярная) |
 |
 |
| Другие |
| Таблица 19.2 |
 |
для привода звена 2 - простейший кулисный механизм, образованный звеньями 4,5 и 2; для привода звена 3 - цепь, состоящая из кулисного механизма (звенья 6,7 и 8) и шарнирного четырехзвенника (звенья 8,9,2 и 3). Таким образом, в рычажном механизме можно выделить кинематическую цепь руки (звенья 1,2 и 3) и кинематические цепи приводов.
Манипуляторы использующие принцип размещения приводов на основании имеют более сложные механизмы. Однако увеличение числа звеньев и кинематических пар компенсируется уменьшением масс и моментов инерции, подвижных звеньев манипулятора. Кроме того, замкнутые кинематические цепи повышают точность и жесткость механизма. В целом манипуляторы, использующие принципы комбинированного размещения приводов (часть приводов на основании, часть на подвижных звеньях), обладают лучшими энергетическими и динамическими характеристиками, а также более высокой точностью.
В кинематических схемах рассмотренных манипуляторов веса звеньев вызывают дополнительную нагрузку на приводы. Фирма SKILAM разработала робот SANCIO (рис. 19.8) в котором веса приводов и звеньев воспринимаются кинематическими парами, а на момент двигателей влияют только через силы трения. Такая структурная схема механизма потребовала увеличения размеров кинематических пар, однако в целом был получен существенный выигрыш по энергетическим и динамическим показателям.
Данные примеры не охватывают всех возможных ситуаций рационального выбора структуры манипуляторов. Они только демонстрируют наиболее известные из удачных структурных схем.
 |
|
| Рис. 19.7 | Рис. 19.8 |
Быстродействие ПР определяют максимальной скоростью линейных перемещений центра схвата манипулятора. Различают ПР с малым (VM<0.5 м/с), средним (0.5 < VM < 1.0 м/с) и высоким (VM>1.0м/с) быстродействием. Современные ПР имеют в основном среднее быстродействие и только около 20% - высокое.
Точность манипулятора ПР характеризуется абсолютной линейной погрешностью позиционирования центра схвата. Промышленные роботы делятся на группы с малой (D rM< 1 мм), средней (0.1 мм < D rM < 1 мм) и высокой (D rM< 0.1 мм) точностью позиционирования.
Режимы движения машины
|
Краткое содержание: Режимы движения машины. Режим движения пуск-останов. Определение управляющих сил по параметрам движения при пуске и останове. Алгоритм решения прямой задачи динамики при неустановившемся режиме движения машины.
Режимы движения машины.
В зависимости от того какую работу совершают внешние силы за цикл движения машины различают три режима движения: разгон, торможение и установившееся движение. Циклом называют период времени или период изменения обобщенной координаты через который все параметры системы принимают первоначальные значения.


























































































































































